В первой части мы описали свойства нейронов. Во второй говорили об основных свойствах, связанных с их обучением. Уже в следующей части мы перейдем к описанию того как работает реальный мозг. Но перед этим нам надо сделать последнее усилие и воспринять еще немного теории. Сейчас это скорее всего покажется не особо интересным. Пожалуй, я и сам бы заминусовал такой учебный пост. Но вся эта «азбука» сильно поможет нам разобраться в дальнейшем.
Персептрон
В машинном обучении разделяют два основных подхода: обучение с учителем и обучение без учителя. Описанные ранее методы выделения главных компонент – это обучение без учителя. Нейронная сеть не получает никаких пояснений к тому, что подается ей на вход. Она просто выделяет те статистические закономерности, что присутствуют во входном потоке данных. В отличие от этого обучение с учителем предполагает, что для части входных образов, называемых обучающей выборкой, нам известно, какой выходной результат мы хотим получить. Соответственно, задача – так настроить нейронную сеть, чтобы уловить закономерности, которые связывают входные и выходные данные.
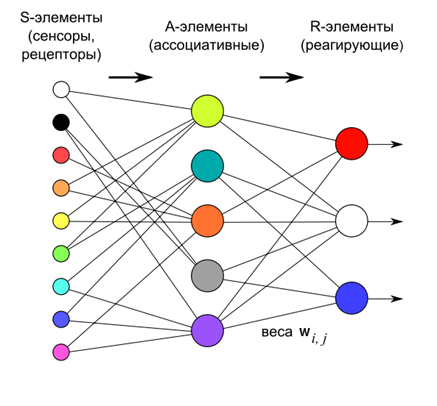
В 1958 году Фрэнк Розенблатт описал конструкцию, названную им персептроном (Rosenblatt, 1958), которая способна к обучению с учителем (смотри КДПВ).
По Розенблатту персептрон состоит из трех слоев нейронов. Первый слой – это сенсорные элементы, которые задают, что же мы имеем на входе. Второй слой – ассоциативные элементы. Их связи с сенсорным слоем жестко заданы и определяют переход к более общей, чем на сенсорном слое, ассоциативной картине описания.
Обучение персептрона осуществляется за счет изменения весов нейронов третьего реагирующего слоя. Цель обучения – заставить персептрон правильно классифицировать подаваемые образы.
Нейроны третьего слоя работают как пороговые сумматоры. Соответственно, веса каждого из них определяют параметры некой гиперплоскости. Если есть линейно-разделимые входные сигналы, то выходные нейроны как раз и могут выступать как их классификаторы.
Если
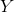 – это вектор реального выхода персептрона а,
– это вектор реального выхода персептрона а, 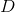 – вектор, который мы ожидаем получить, то о качестве работы нейронной сети говорит вектор ошибки:
– вектор, который мы ожидаем получить, то о качестве работы нейронной сети говорит вектор ошибки: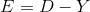
Если задаться целью, минимизировать среднеквадратическую ошибку, то можно вывести так называемое дельта-правило модификации весов:
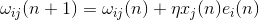
При этом начальным приближением могут выступать нулевые веса.
Это правило является не чем иным, как правилом Хебба, примененным к случаю персептрона.
Если за выходным слоем расположить еще один или несколько реагирующих слоев и отказаться от ассоциативного слоя, который был введен Розенблаттом более для биологической достоверности, чем из-за вычислительной необходимости, то мы получим многослойный персептрон такой, как показан на рисунке ниже.
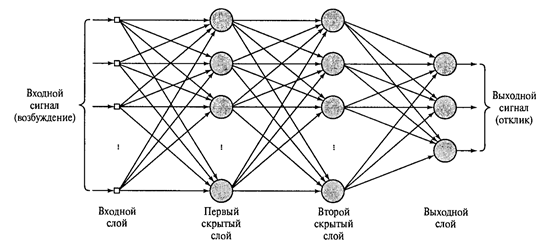
Многослойный персептрон с двумя скрытыми слоями (Хайкин, 2006)
Если бы нейроны реагирующих слоев были простыми линейными сумматорами, то большого смысла в таком усложнении не было бы. Выход, независимо от числа скрытых слоев, все равно оставался бы линейной комбинацией входных сигналов. Но поскольку в скрытых слоях используются пороговые сумматоры, то каждый такой новый слой разрывает цепочку линейности и может нести свое интересное описание.
Долгое время было непонятно, как можно обучать многослойный персептрон. Основной метод – метод обратного распространения ошибки был описан только в 1974 г. А.И. Галушкиным и независимо и одновременно Полом Дж. Вербосом. Затем он был переоткрыт и получил широкую известность в 1986 г. (David E. Rumelhart, Geoffrey E. Hinton, Ronald J. Williams, 1986).
Метод состоит из двух проходов: прямого и обратного. При прямом проходе подается обучающий сигнал и рассчитывается активность всех узлов сети, включая активность выходного слоя. Вычитанием полученной активности из того, что требовалось получить, определяется сигнал ошибки. При обратном проходе сигнал ошибки распространяется в обратном направлении, от выхода ко входу. При этом синаптические веса настраиваются с целью минимизации этой ошибки. Подробное описание метода можно найти во множестве источников (например, Хайкин, 2006).
Нам важно обратить внимание на тот факт, что в многослойном персептроне информация обрабатывается от уровня к уровню. При этом каждый слой выделяет свой набор признаков, свойственных входному сигналу. Это создает определенные аналогии с тем, как преобразуется информация между зонами коры головного мозга.
Сверточные сети. Неокогнитрон
Сравнение многослойного персептрона и реального мозга очень условно. Общее – это то, что, поднимаясь от зоны к зоне в коре или от слоя к слою в персептроне, информация приобретает все более обобщенное описание. Однако строение участка коры значительно сложнее, чем организация слоя нейронов в персептроне. Исследования зрительной системы Д. Хьюбела и Т. Визела позволили лучше понять строение зрительной коры и подтолкнули к использованию этих знаний в нейронных сетях. Основные идеи, которые были использованы – это локальность зон восприятия и деление нейронов по функциям внутри одного слоя.
Локальность восприятия нам уже знакома, она означает, что нейрон, получающий информацию, следит не за всем входным пространством сигналов, а только за его частью. Ранее мы говорили, что такая область слежения называется рецептивным полем нейрона.
Понятие рецептивного поля требует отдельного уточнения. Традиционно рецептивным полем нейрона принято называть то пространство рецепторов, которое влияет на работу нейрона. Под рецепторами здесь понимаются нейроны, непосредственно воспринимающие внешние сигналы. Представим нейронную сеть, состоящую из двух слоев, где первый слой – слой рецепторов, а второй слой – нейроны, соединенные с рецепторами. Для каждого нейрона второго слоя те рецепторы, что имеют с ним контакт – это и есть его рецептивное поле.
Теперь возьмем сложную многослойную сеть. Чем дальше мы будем уходить от входа, тем сложнее будет указать, какие рецепторы и как влияют на активность находящихся в глубине нейронов. С определенного момента может оказаться, что для какого-либо нейрона все существующие рецепторы могут быть названы его рецептивным полем. В такой ситуации рецептивным полем нейрона хочется назвать только те нейроны, с которыми он имеет непосредственный синаптический контакт. Чтобы развести эти понятия, будем называть пространство входных рецепторов – исходным рецептивным полем. А то пространство нейронов, что взаимодействует с нейроном непосредственно – локальным рецептивным полем или просто рецептивным полем, без дополнительного уточнения.
Деление нейронов на функции связано с обнаружением в первичной зрительной коре двух основных типов нейронов. Простые (simple) нейроны реагируют на стимул, расположенный в определенном месте их исходного рецептивного поля. Сложные (complex) нейроны проявляют активность на стимул, независимо от его положения.
Например, на рисунке ниже показаны варианты того, как могут выглядеть картины чувствительности исходных рецептивных полей простых клеток. Положительные области активируют такой нейрон, отрицательные подавляют. Для каждого простого нейрона есть стимул, наиболее подходящий для него и, соответственно, вызывающий максимальную активность. Но важно то, что этот стимул жестко привязан к позиции на исходном рецептивном поле. Такой же стимул, но смещенный в сторону, не вызовет реакции простого нейрона.
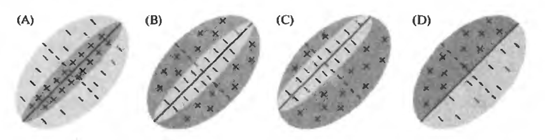
Исходные рецептивные поля простой клетки (Николлс Дж., Мартин Р., Валлас Б., Фукс П.)
Сложные нейроны также имеют предпочитаемый ими стимул, но способны узнать этот стимул независимо от его положения на исходном рецептивном поле.
Из этих двух идей родились соответствующие модели нейронных сетей. Первую подобную сеть создал Кунихика Фукусима. Она получила название когнитрон. Позже он создал более продвинутую сеть – неокогнитрон (Fukushima, 1980). Неокогнитрон – это конструкция из несколько слоев. Каждый слой состоит из простых (s) и сложных (с) нейронов.
Задача простого нейрона следить за своим рецептивным полем и узнавать образ, на который он обучен. Простые нейроны собраны в группы (плоскости). Внутри одной группы простые нейроны настроены на один и тот же стимул, но каждый нейрон следит за своим фрагментом рецептивного поля. Все вместе они перебирают все возможные положения этого образа (рисунок ниже). Все простые нейроны одной плоскости имеют одинаковые веса, но разные рецептивные поля. Можно представить ситуацию по-другому, что это один нейрон, который умеет примерять свой образ сразу ко всем позициям исходной картинки. Все это позволяет узнавать один и тот же образ независимо от его положения.
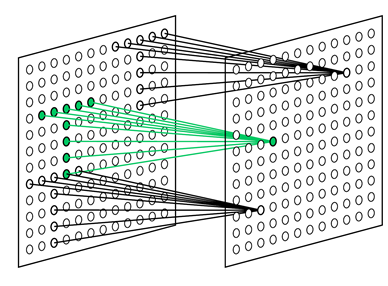
Рецептивные поля простых клеток, настроенных на поиск выбранного паттерна в разных позициях (Fukushima K., 2013)
Каждый комплексный нейрон следит за своей плоскостью простых нейронов и срабатывает, если активен хотя бы один из простых нейронов в его плоскости (рисунок ниже). Активность простого нейрона говорит о том, что он узнал характерный стимул в том конкретном месте, которое является его рецептивным полем. Активность комплексного нейрона означает, что тот же образ встретился вообще на слое, за которым следят простые нейроны.
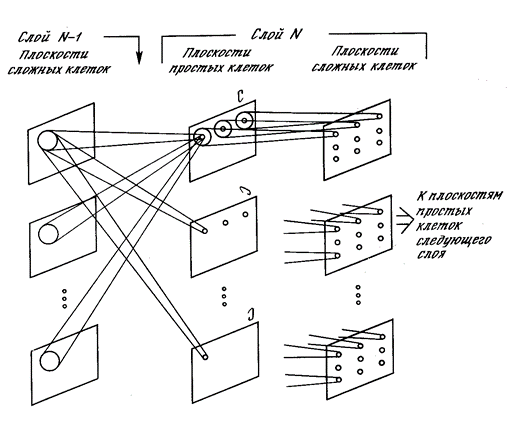
Плоскости неокогнитрона
Каждый слой после входного имеет своим входом картину, образованную комплексными нейронами предыдущего слоя. От слоя к слою происходит все большее обобщение информации, которое в результате приводит к распознаванию конкретных образов независимо от их расположения на исходной картинке и некоторой трансформации.
Применительно к анализу изображений это означает, что первый уровень распознает линии под определенным углом, проходящие через небольшие рецептивные поля. Он способен детектировать все возможные направления в любом месте изображения. Следующий уровень детектирует возможные сочетания элементарных признаков, определяя более сложные формы. И так до того уровня, пока не удастся определить требуемый образ (рисунок ниже).

Процесс распознавания в неокогнитроне
При использовании для распознавания рукописного текста такая конструкция оказывается устойчива к способу написания. На успешность распознавания не влияет ни перемещение по поверхности или поворот, ни деформация (растяжение или сжатие).
Самое существенное отличие неокогнитрона от полносвязанного многослойного персептрона – это значительно меньшее количество используемых весов при том же количестве нейронов. Так получается за счет «трюка», который позволяет неокогнитрону определять образы независимо от их положения. Плоскость простых клеток – это по сути один нейрон, веса которого определяют ядро свертки. Это ядро применяется к предыдущему слою, пробегая его во всех возможных позициях. Собственно нейроны каждой плоскости и задают своими связями координаты этих позиций. Это приводит к тому, что все нейроны слоя простых клеток следят за тем, не появится ли в их рецептивном поле образ, соответствующий ядру. То есть, если такой образ встретится где-либо во входном для этого слоя сигнале, это будет обнаружено хотя бы одним простым нейроном и вызовет активность соответствующего сложного нейрона. Это ухищрение позволяет найти характерный образ в любом месте, где бы он ни появился. Но надо помнить, что это именно ухищрение и оно не особо соответствует работе реальной коры.
Обучение неокогнитрона происходит без учителя. Оно соответствует описанной ранее процедуре выделения полного набора факторов. Когда на вход неокогнитрона подаются реальные изображения, нейронам не остается ничего другого, кроме как выделять свойственные этим изображениям компоненты. Так, если подавать на вход рукописные цифры, то малые рецептивные поля простых нейронов первого слоя увидят линии, углы и сопряжения. Размеры зон конкуренции определяют, сколько различных факторов может выделиться в каждой пространственной области. В первую очередь выделяются наиболее значимые компоненты. Для рукописных цифр это будут линии под различными углами. Если останутся свободные факторы, то далее могут выделиться и более сложные элементы.
От слоя к слою сохраняется общий принцип обучения – выделяются факторы, характерные для множества входных сигналов. Подавая рукописные цифры на первый слой, на определенном уровне мы получим факторы, соответствующие этим числам. Каждая цифра окажется сочетанием устойчивого набора признаков, что выделится как отдельный фактор. Последний слой неокогнитрона содержит столько нейронов, сколько образов предполагается детектировать. Активность одного из нейронов этого слоя говорит об узнавании соответствующего образа (рисунок ниже)
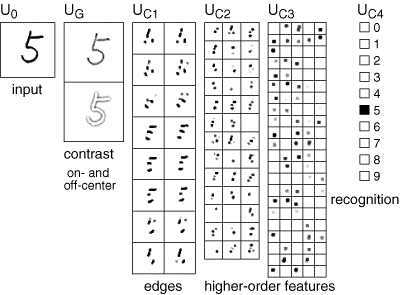
Распознавание в неокогнитроне (Fukushima K., Neocognitron, 2007)
Видео ниже позволяет получить наглядное представление о неокогнитроне.
Альтернатива обучению без учителя – это обучение с учителем. Так, в примере с цифрами мы можем не ждать, пока сеть сама выделит статистически устойчивые формы, а говорить ей, что за цифра ей предъявляется, и требовать соответствующего обучения. Наиболее значительных результатов в таком обучении сверточных сетей добился Ян ЛеКун (Y. LeCun and Y. Bengio, 1995). Он показал, как можно использовать метод обратного распространения ошибки для обучения сетей, архитектура которых, как и у неокогнитрона, отдаленно напоминает строение коры мозга.

Сеть свертки для распознавания рукописного текста (Y. LeCun and Y. Bengio, 1995)
На этом будем считать, что минимальные начальные сведения напомнены и можно перейти к вещам более интересным и удивительным.
Продолжение
Предыдущие части:
Часть 1. Нейрон
Часть 2. Факторы






