
Есть мнение, что в оптимальной компоновке многоступенчатой ракеты каждая ступень должна иметь запас характеристической скорости (delta-V) в 4 км/с. Считается, что оптимальная начальная тяговооруженность 1.2. Но эти идеи надо как-нибудь подтвердить. Также мне хотелось наглядно показать, почему ракеты делают многоступенчатыми. Формулы — это хорошо, но нужно ещё что-то интересное, и в качестве такого идеально подходят игры и соревнования. Так родился проект образовательной/игровой программы под кодовым названием «enlarge your ПН»
Постановка задачи и принятые упрощения
Виртуально разгонять ракету в вакууме вдали от планет мне показалось неинтересным. Поэтому задачей будет стартовать с Земли. Расчет аэродинамического сопротивления и выхода на орбиту с поверхности представился сложным, поэтому ракета, как в мысленном эксперименте Ньютона, будет стартовать с «высокой горы» в вакууме:
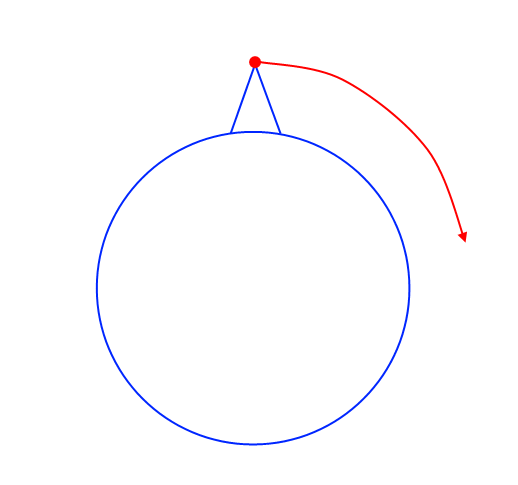
Входные параметры
В качестве входных данных были выбраны следующие параметры:
- Сухая масса двигателей, кг.
- Количество двигателей, штук.
- Тяга двигателей в килоньютонах.
- Расход всех компонентов топлива одним двигателем, килограмм в секунду.
- Масса топлива, кг.
Расчетные и связанные параметры
Те, кто хотя бы чуть-чуть интересовался ракетной техникой, могут спросить, куда пропал удельный импульс, который используется в формуле Циолковского? На самом деле, он никуда не пропал. Удельный импульс неявно содержится в тяге двигателя и расходе топлива. УИ пропорционален тяге и обратно пропорционален расходу топлива. Чем больше тяга и чем меньше расход топлива, тем больше УИ.
Тягу двигателя в тоннах можно пересчитать в тягу в килоньютонах, умножив её на 9,81.
Масса баков, переходников и прочих вспомогательных конструкций считается «навскидку» как 10% массы топлива и названа «паразитной массой». Это достаточно серьезное упрощение, потому что в реальности этот параметр сильно влияет на общую эффективность ракеты и отличается у разных ракет. Чем легче баки, переходники и прочие конструкции, тем меньше паразитной массы надо поднимать ракете.
Полная и пустая массы рассчитываются на базе известных параметров. Пустая масса — это масса всех двигателей и паразитная масса, полная масса — это пустая масса и масса топлива
Расчет гравитационных потерь подробно показан ниже.
Не учитывающиеся параметры
- Для упрощения задачи не учитываются:
- Потери на трение о воздух.
- Изменение тяги в зависимости от атмосферного давления.
- Набор высоты.
- Потери времени на разделение ступеней.
- Изменения тяги двигателей на участке максимального скоростного напора.
- Учитывается только одна компоновка — с последовательным расположением ступеней.
Немного физики и математики
Расчет скорости
Разгон ракеты в модели происходит так:

Высота полёта предполагается постоянной. Тогда тягу ракеты можно будет разделить на две проекции: Fx и Fy. Fy должен быть равен mg, это наши гравитационные потери, а Fx — это сила, которая будет разгонять ракету. F постоянна, это тяга двигателей, m меняется из-за расхода топлива.
Изначально была попытка аналитического решения уравнения движения ракеты. Однако, она не увенчалась успехом, поскольку гравитационные потери зависят от скорости ракеты. Проведем мысленный эксперимент:
- В начале полёта ракета просто не оторвется от стартового стола, если тяга двигателей будет меньше, чем вес ракеты.
- В конце разгона ракета всё также притягивается к Земле с силой mg, но это неважно, поскольку её скорость такая, что упасть она не успевает, и, когда она выйдет на круговую орбиту, она будет постоянно падать на Землю, «промахиваясь» мимо неё из-за скорости.
Получается, что фактические гравитационные потери являются функцией от массы и скорости ракеты. В качестве упрощённого приближения гравитационные потери я решил считать как:

V1 — это первая космическая скорость.
Для расчета итоговой скорости пришлось использовать численное моделирование. С шагом в одну секунду производятся следующие расчеты:
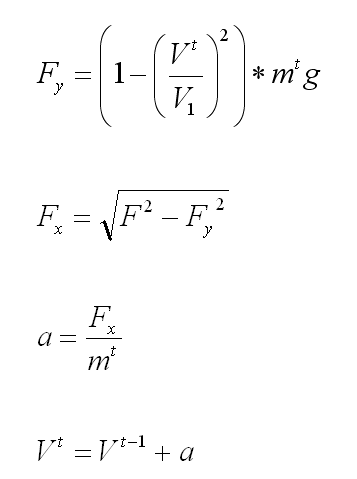
Верхний индекс t — это текущая секунда, t-1 — предыдущая.
Или на языке программирования
for (int time = 0; time < iBurnTime[stage]; time++) {
int m1 = m0 - iEngineFuelUsage[stage] * iEngineQuantity[stage];
double ms = ((m0 + m1) / 2);
double Fy = (1-Math.pow(result/7900,2))*9.81*ms;
if (Fy < 0) {
Fy = 0;
}
double Fx = Math.sqrt(Math.pow(iEngineThrust[stage] * iEngineQuantity[stage] * 1000, 2)-Math.pow(Fy, 2));
if (Fx < 0) {
Fx = 0;
}
result = (result + Fx / ms);
m0 = m1;
}
Расчет максимальной полезной нагрузки
Зная итоговую скорость для каждой допустимой полезной нагрузки, можно решать задачу максимизации полезной нагрузки как задачу нахождения корня нелинейного уравнения.

Мне показалось удобнее всего решать это уравнение методом половинного деления:
Код совершенно стандартный
public static int calculateMaxPN(int stages) {
deltaV = new double[5];
int result = 0;
int PNLeft = 50;
while (calculateVelocity(PNLeft, stages, false) > 7900) {
PNLeft = PNLeft + 1000;
}
System.out.println(calculateVelocity(PNLeft, stages, false));
int PNRight = PNLeft - 1000;
double error = Math.abs(calculateVelocity(PNLeft, stages, false) - 7900);
System.out.println("Слева " + Double.toString(PNLeft) + "; Справа " + Double.toString(PNRight) + "; Ошибка " + Double.toString(error));
boolean calcError = false;
while ((error / 7900 > 0.001) && !calcError) {
double olderror = error;
if (calculateVelocity((PNLeft + PNRight) / 2, stages, false) > 7900) {
PNRight = (PNLeft + PNRight) / 2;
} else {
PNLeft = (PNLeft + PNRight) / 2;
}
error = Math.abs(calculateVelocity((PNLeft + PNRight) / 2, stages, false) - 7900);
System.out.println("Слева " + Double.toString(PNLeft) + "; Справа " + Double.toString(PNRight) + "; Ошибка " + Double.toString(error));
if (Math.abs(olderror - error) < 0.0001) { //аварийный выход если алгоритм уйдет не туда
PNLeft = 0;
PNRight = 0;
calcError = true;
}
}
result = (PNLeft + PNRight) / 2;
calculateVelocity(result, stages, true);
return result;
}
А поиграть?
Теперь, после теоретической части, можно и поиграть.
Проект расположен на GitHub. Лицензия MIT, пользуйтесь и модифицируйте на здоровье, а распространение даже приветствуется.
Если вдруг кому нужна инструкция по установке
- Пройти по ссылке https://github.com/lozga/rocketcalc
- Скачать архив по кнопке «Download ZIP».
- Распаковать в какую-нибудь папку.
- Если у вас не установлена Java, поставьте её с оф. сайта.
- Запустить файл RocketStageCalc.jar.
Главное и единственное окно программы:
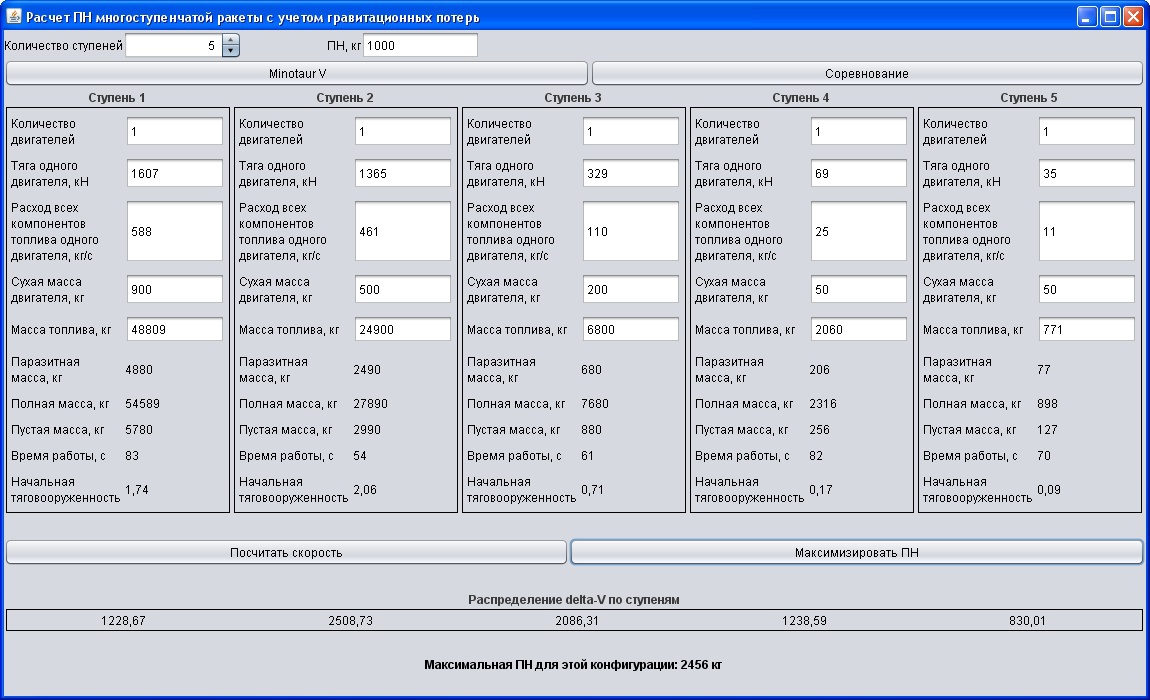
Вы можете рассчитать конечную скорость ракеты для указанной ПН, заполнив текстовые поля параметров, введя ПН сверху и нажав кнопку «Посчитать скорость».
Также можно рассчитать максимальную полезную нагрузку для данных параметров ракеты, в этом случае поле «ПН» не учитывается.
Есть реальная ракета с пятью ступенями «Minotaur V». Кнопка «Minotaur V» загружает параметры, похожие на эту ракету для того, чтобы показать пример работы программы.
По сути это режим «песочницы», в котором можно создавать ракеты с произвольными параметрами, изучая, как различные параметры влияют на грузоподъемность ракеты.
Соревнование
Режим «Соревнование» активируется нажатием кнопки «Соревнование». В этом режиме количество управляемых параметров сильно ограничено для одинаковости условий соревнования. На всех ступенях стоят однотипные двигатели (это нужно для наглядности необходимости нескольких ступеней). Можно управлять количеством двигателей. Также можно управлять распределением топлива по ступеням и количеством ступеней. Максимальный вес топлива — 300 тонн. Залить меньше топлива можно.
Задача: используя минимальное количество двигателей добиться максимальной ПН. Если желающих поиграть будет много, то в каждом количестве двигателей будет свой зачет.
Желающие могут оставлять свой результат с использованными параметрами в комментариях. Успехов!
UPD: Сасибо 0serg, улучшил формулы.













