Всем хаброжителям доброго времени суток!
В этой статье вы сможете узнать, как настроить IBM Security Network Protection (XGS5100) в основанной на Open vSwitch программно-конфигурируемой сети(SDN), и защитить-таки все ваши виртуальные активы.
Open vSwitch — это виртуальный коммутатор на основе OpenFlow, широко используемый в облачных средах.
Software-defined Networking (SDN) — это технология для развертывания облака, обеспечивающая масштабируемую и гибкую среду, подходящую для динамического характера этого самого облака.
Вы научитесь разворачивать IBM Security Network Protection (ISNP) в рамках OpenFlow с поддержкой SDN коммутатора — Open vSwitch и увидите как легко ISNP могут быть развернуты в среде SDN.

SDN – новый архитектурный подход, цель которого обеспечить сетевую гибкость, подходящую для динамики современной среды. Существующие сетевые технологии являются по своей сути статическими и их трудно изменить, так как небольшие сетевые изменения часто требуют существенной переконфигурации всех, или большей части коммутаторов, маршрутизаторов и межсетевых экранов. Мало того, что
процесс этот занимает много времени для администратора и не решается при помощи одного лишь бубна, он еще и несет в себе опасность получить кучу ошибок.
В архитектуре программно-конфигурируемой сети выделяется два уровня:
инфраструктурный уровень, на котором функционируют сетевые коммутаторы и каналы передачи данных, и уровень управления — набор программных средств, физически отделённых от инфраструктурного уровня, обеспечивающий реализацию механизмов управления устройствами инфраструктурного уровня.
В традиционных сетях уровень управления реализуется в устройствах передачи данных, и эта реализация зависит от поставщика.
В SDN эти уровни разделены,
управление осуществляется централизованно для всего сетевого оборудования в рамках предприятия (независимо от производителя оборудования). Эта архитектура обеспечивает простой и быстрый способ для управления потоком трафика.
Облачные среды требуют динамического распределения ресурсов. Открытые и частные облака имеют виртуальные приложения и хранилища, так что следующий логический шаг – это виртуализация сети. А почему бы и нет?!
SDN дает платформу, обеспечивающую сетевую виртуализацию, что дает возможность создать полностью динамическую среду для хранения данных, сети и приложений.
SDN требует взаимодействия централизованного уровня управления с инфраструктурным уровнем (реализованным в физических устройствах). Протокол OpenFlow от Open Networking Foundation – это протокол SDN, обеспечивающий такую связь. OpenFlow позволяет детально контролировать трафик на всех коммутаторах и маршрутизаторах в сети, как
физических, так и виртуальных, независимо от поставщика программного
обеспечения.
Таким образом протокол OpenFlow устраняет необходимость конфигурирования устройства каждого поставщика в отдельности через собственный интерфейс.
Open vSwitch представляет из себя виртуальный коммутатор под лицензией Apache 2.0. Он, как правило, устанавливается на сервере для контроля трафика в гипервизоре, обеспечивая динамическую сетевую среду.
Open vSwitch поддерживает ряд протоколов для управления трафиком, в том числе NetFlow, sFlow, SPAN, RSPAN, CLI, 802.1ag и OpenFlow.
ISNP – продукт объединяющий функции системы предотвращения вторжений и сложного контроля за приложениями.
Он дает возможность контроля над всей активностью пользователя, анализируя каждое соединение и определяя используемые приложения. В зависимости от репутации приложения ISNP может позволить или заблокировать соединение. Также ISNP может записывать информацию приложений, что может быть полезным для уточнения политики, включая пропускную способность.
Интегрированная с другими защитными функциями система предотвращения вторжений обеспечивает быструю развертку и простое администрирование.
Подготовка
Мы будем использовать 64-битный Ubuntu 12.04 LTS с поддержкой до апреля 2017. Мы устанавливали Ubuntu на «голое железо», а не на виртуальной машине. Использование «голого железа» для установки KVM гипервизора дает хорошую производительность для VM.
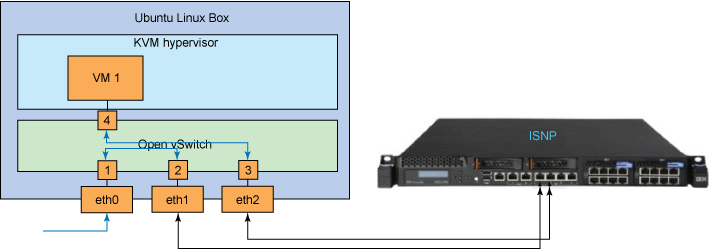
Сервер должен иметь как минимум три сетевых интерфейса: один для удаленного доступа, и два для подключения к
ISNP напрямую к портам защиты(как показано на Рис.1).
Рис.1
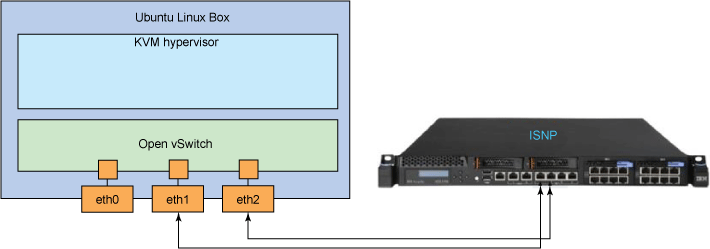
Виртуальная машина (KVM) является инфраструктурой виртуализаци для ядра Linux, и превращает его в гипервизор.
Перед тем как заняться установкой Ubuntu, активируйте набор команд VT-d в ЦПУ, в настройках BIOS,
Рекомендуемый дистрибутив – Ubuntu 12.04 LTS.
После загрузки системы на жесткий диск, вам будет предложено выбрать дополнительные компоненты Ubuntu “из коробки”.
В разделе software selection необходимо выбрать Virtual Machine host и OpenSSH server
Рис.2
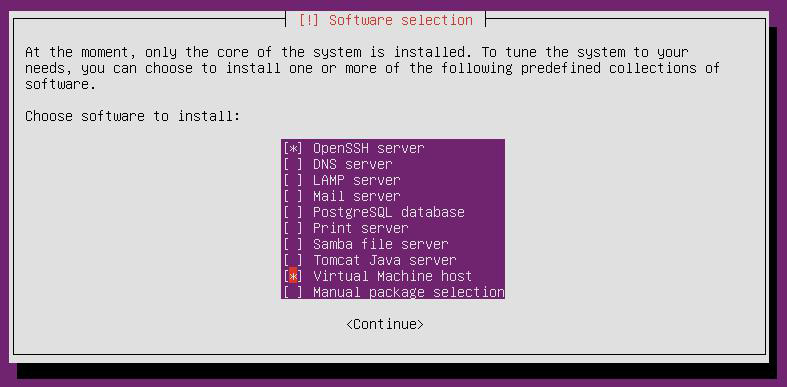
Для меня, а так же для всех неожиданно ослепших или промахнувшихся мимо нужной строки, или еще по каким либо причинам забывших выбрать Virtual Machine host, есть возможность установить необходимые компоненты KVM с помощью следующей команды: # sudo apt-get install qemu-kvm libvirt-bin.
Для завершения установки KVM гипервизора, выполните следующие действия:
Затем, введите /etc/libvirt/qemu.conf и добавьте следующие параметры:
НЕ ЗАБУДЬТЕ РАСКОММЕНТИРОВАТЬ ВЫШЕУКАЗАННЫЕ НАСТРОЙКИ (УДАЛИТЬ # В НАЧАЛЕ КАЖДОЙ СТРОКИ)
Перезапустите libvirt-bin для загрузки и установки qemu настроек: # sudo service libvirt-bin restart.
При желании вы можете установить virt-manager : # sudo apt-get install virt-manager. Утверждается, что у него удобный интерфейс для настройки виртуальных машин.
Чтобы настроить Open vSwitch, вам придется установите все необходимые компоненты Open vSwitch (Подойдет Open vSwitch 1.4.0 ):
Примечание: при установке этих пакетов на ядре 3.8 вы можете столкнуться некоторыми проблемами, но сотрудники Ubuntu усердно трудятся над их решениям, пока я пишу статью. А теперь о приятном – в ядре 3.8 уже есть нативный openvswitch module, по этому нет необходимости самим собирать его.
Как только openvswitch module будет загружен, так сразу ваша система будет готова к использованию.
Ах да, убедитесь что вы все таки загрузили openvswitch module и вам это не приснилось: # lsmod | grep openvswitch . А если вы вдруг захотите проверить запущены ли ovsdb-server и ovs-vswitchd, то используйте эту команду: # sudo service openvswitch-switch status
Вы должны увидеть это:
Конфигурирование Open vSwitch
Следующий шаг демонстрирует как сконфигурировать Open vSwitch и использовать интерфейс eth0 как порт uplink
После этого Виртуальные Машины подключатся к коммутатору и получат доступ к сети.
Чтобы еще раз убедиться в том, что вы «умничка», ваш Open vSwitch готов к использованию и вы все сделали правильно, выполните эти команды:
Вы должны увидеть это:
Убедительная просьба заняться конфигурированием после того, как вы убедитесь что все сервисы Open vSwitch работают корректно.
Сбрасываем настройки eth0:
Создаем новый vSwitch:
Добавляем eth0 на ovs-internal:
Поднимаем ovs-internal:
Устанавливаем IP адрес для ovs-internal:
Статический IP:
DHCP:
Добавляем eth1 и eth2 к ovs-internal. Вводим команды в указанном порядке:
После введения этих команд происходит деактивация сетевых интерфейсов eth1 и eth2 и устанавка на них опции noflood.
Необходимо соблюдать порядок ввода команд, не то получите loop. Эти 2 порта заработают, когда устройство ISNP готово и кабели воткнуты в eth1 и eth2.
После того, как установка Open vSwitch будет завершена вы можете воспользоваться ovs-vsctl и увидеть статус ваших коммутаторов.
Если вы не хотите каждый раз настраивать Open vSwitch зайдите /etc/network/interfaces и добавьте «постоянные» настройки
Для статической конфигурации IP, необходимо изменить настройки так, чтобы было похоже на это:
А для того чтобы сконфигурировать DHCP, настройки должны быть похожи на это:
Важно установить noflood на eth1 и eth2. В /etc/network/interfaces делать это не желательно, поэтому вам будет необходимо ввести следующие команды в /etc/rc.local:
Настройте свой ISNP и подключите eth1 и eth2 к портам устройства (как показано на рисунке 1 ).
Когда установка завершиться, вы сможете войти в интерфейс и увидеть панель управления ISNP.
Рис.3
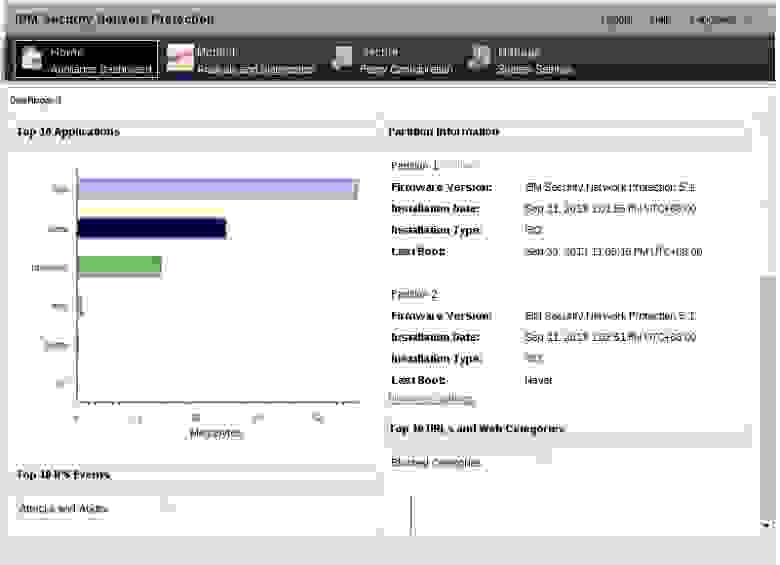
Для этой статьи ISNP использовался как IPS. Мы использовали стоявшую по умолчанию X-Force IPS, а не сетевую политику контроля пользователей и приложений. В итоге было активировано только правило «any any». Остальные правила, указанные в начальных настройках поставляются вместе с XGS5100(версия 5.1)
Рис.4
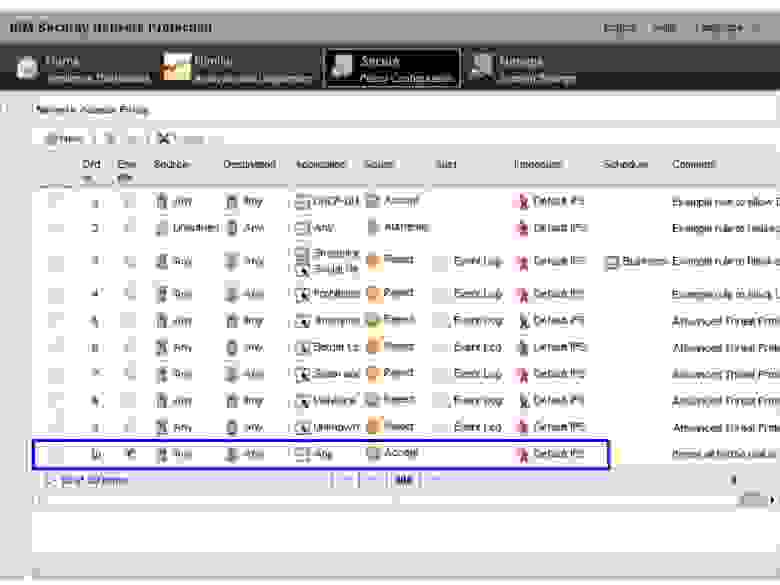
После настройки ISNP подключите кабели и поднимите eth1 и eth2 порты на ovs-internal:
Перепроверьте правильно ли вы установили noflood на eth1 и eth2, потому что если нет, то при подключении кабелей получите loop.
Для начала вам необходимо приготовить скрипт для подключения вашей виртуальной NIC на вашей виртуальной машине к ovs-internal.
Скопируйте этот код в /etc/ovs-ifup:
Добавьте разрешение на исполнение скрипта: # sudo chmod +x /etc/ovs-ifup.
Для создания виртуальной машины воспользуйтесь virt-manager. Так как здесь использовался Ubuntu 12.04 server и мы не установили X-сервер, то мы не сможем запустить какую либо программу с GUI.
Но если вдруг вы решили использовать Desktop Edition, то проблема будет решена и вы можете получить доступ к virt-manager напрямую.
Для запуска virt-manager на вашей KVM, используйте X forwarding(для просмотра GUI программ на вашем локальном сервере)
Если вы работаете под Linux, то для соединения с удаленным KVM необходимо запустить команду активирующую X forwarding. (Соединение X forwarding с сервером по протоколу SSH): # ssh -X user@<server_ip>.>.
Вместо eth0 вам необходимо получить IP-адрес вашего сервера от ovs-internal : # ifconfig ovs-internal>.
После входа на удаленный KVM, запустите virt-manager: # virt-manager.
Если все правильно, то отобразится GUI программы.
Рис.5
Теперь создаем первую виртуальную машину.
Рис.6
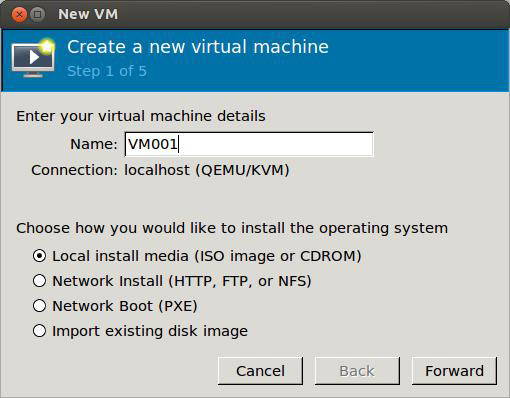
Рис.7
У нее должен быть хотя бы один vNIC (Virtualized Network Interface)
Рис.8
vNIC будут отконфигурированы позже, а пока закройте созданную виртуальную машину и вручную измените ее XML-файл:Edit /etc/libvirt/qemu/.xml.
Изначально настройки XML-файла должны выглядеть так:
Измените настройки XML-файла, чтобы он выглядел так:
Отдайте команду KVM загрузить обновленный XML-файл: # sudo virsh define /etc/libvirt/qemu/.xml.
Все! «Властвуйте и разделяйте» на созданной вами виртуальной машине.
Выполнив следующие команды вы должны увидеть созданный порт на ovs-internal.
Попробуйте установить на вашу виртуальную машину любую операционную систему и попытайтесь подключиться к сети.
Когда ваша виртуальная машина соединена с Open vSwitch на ней должны работать сеть(в режиме моста) и DHCP сервер. Если DHCP сервер не доступен, то вам придется назначить IP адрес виртуальной машине вручную.
Из-за ошибки в Libvirt, ovs-ifdown скрипт не указан в файле описания. Необходимо выключить виртуальную машину и отключить tap (Ethernet) устройство от коммутатора. Если этого не сделать, то сообщение об ошибке будет появляться и при последующих запусках виртуальной машины.
Рис.9
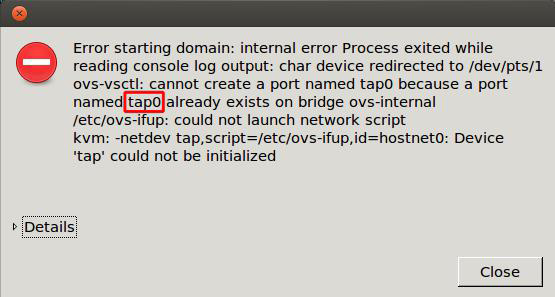
Чтобы отключить tap устройство от ovs-internal необходимо ввести эту команду: # sudo ovs-vsctl del-port ovs-internal tapN.
из сообщения об ошибке мы можем узнать какое устройство отключено от коммутатора. (Рис.9)
Теперь необходимо «обучить» ovs-internal проверке пакетов, при передаче трафика в ISNP. Используйте команду ovs-ofctl для установки правил SDN на ovs-internal. Структура правил при работе с коммутатором определяется стандартом OpenFlow. Повторите то же самое для защиты других виртуальных машин.
Если вы установили не верные правила, ваша виртуальная машина не сможет пользоваться сетью. Чтобы восстановить подключение к сети необходимо сбросить настройки коммутатора используя следующие команды:
Вы должны знать два атрибута с первой виртуальной машины: МАС-адрес и номер порта через который ваша Виртуальная машина соединяется с ovs-internal.
Посмотреть МАС-адрес вашей виртуальной NIC можно здесь:
/etc/libvirt/qemu/.xml:
Так же можно посмотреть МАС-адрес, присваивающийся каждому сетевому устройству, непосредственно на самой виртуальной машине.
Теперь вам нужен номер порта через который ваша Виртуальная машина соединяется с ovs-internal. Чтобы получить статус порта на ovs-internal необходимо запустить следующую команду: # sudo ovs-ofctl show ovs-internal.
Вывод команды должен выглядеть следующим образом:
Цифры (от 1 до 4) это номер порта, следом в скобках-название подключенного к порту устройства.
Каждое vNIC на виртуальной машине отображается как tap устройство гипервизора. Таким образом, мы можем видеть, что первая виртуальная машина подключена к 4 порту на ovs-internal, eth2 ко 2 порту, и eth3 к 3 порту. Все эти значения вы увидите в правилах управления коммутатором.
Обратите внимание, что номер порта на коммутаторе может быть изменен после перезагрузки сервера.
Необходимо использовать верный номер порта в последующих правилах управления ovs-internal, в противном случае сетевой трафик не будет проходить через ISNP устройства…
Примечание: eth0 не всегда будет находится на первом порту.
Предположим, что MAC-адрес первой Виртуальной Машины 52: 54: 00: AA: BB: CC.
Установите новые правила для ovs-internal.
Правила по правилам
Синие линии, на рис. 10 демонстрируют как как коммутатор пересылает трафик, передаваемый от внешнего компьютера на ISNP, а затем на первую виртуальную машину.
Рис.10
С помощью этой команды вы можете сбросить все текущие правила на ovs-internal и посмотреть как много пакетов «убило» каждое правило: # sudo ovs-ofctl dump-flows ovs-internal.
Вывод должен выглядеть примерно так:
Теперь вы можете проверить работу ISNP и запустить на первой виртуальной машине тесты на проникновение.
В разделе ,«Verify that the ISNP device is protecting your virtual machines» есть несколько простых тестов, для проверки ISNP защиты вашей виртуальной машины
Вторую виртуальную машину вы можете создать путем клонирования первой, используя virt-manager, или вручную, как вы делали ранее
Не забудьте изменить XML-файл, чтобы виртуальная машина автоматически подключаться к ovs-internal
Чтобы получить номер порта, используемого второй Виртуальной Машиной, снова запустите ovs-ofctl команду:# sudo ovs-ofctl show ovs-internal.
Результат будет выглядеть примерно так:
Здесь мы видим что новое tap устройство подключено к ovs-internal через пятый порт.
Предположим, что MAC-адрес второй Виртуальной Машины 52: 54: 00: AA: CC: DD. Необходимо установить следующие правила для ovs-internal, чтобы защитить его от внешнего трафика и от трафика между Виртуальными машинами.
Правила по правилам
Красные линии на рисунке 11 отображают новые правила, установленные для коммутатора(защищающие трафик между двумя виртуальными машинами).
Рис.11

Удостоверьтесь что все правила, установленные для ovs-internal корректны: # sudo ovs-ofctl dump-flows ovs-internal.
Здесь вы так же можете проверить работу ISNP, запустив тестирование на проникновение из одной виртуальной машины на другую.
1)Самый простой способ убедиться, что сетевой трафик пошел через ISNP — это использовать Network Graphs в интерфейсе управления ISNP. Перед тем как Network Graphs начнут проверку необходимо отправить часть трафика на виртуальные машины.
Перед проверкой мы имеем возможность выбрать интересующий нас график.
Рис.12

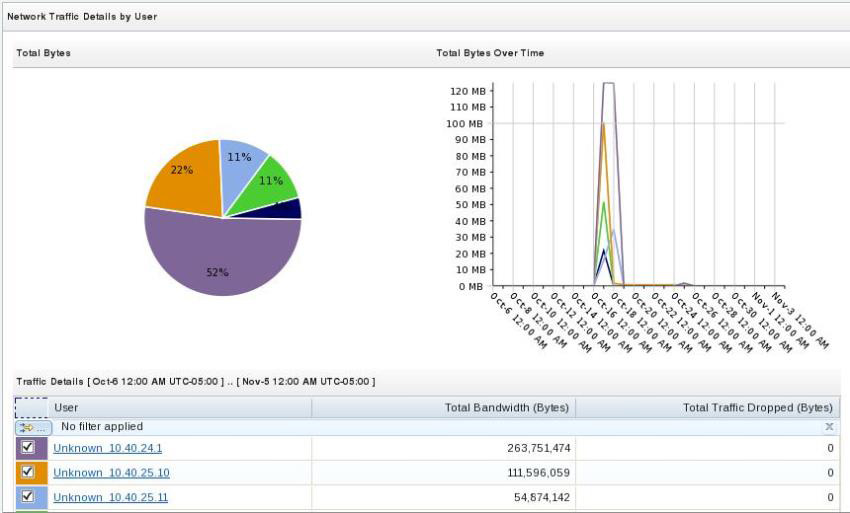
Рекомендовано использовать"Detail by User". В этом случае, если IP-адреса ваших виртуальных машин появятся в сетевой статистике, то график будет похож на то что мы видим на Рис.13
Рис.13
2)Вы можете послать на ваши виртуальные машины безвредную атаку и посмотреть блокирует ли их ваш ISNP.
При корректной работе ISNP атаки будут блокированы, а в интерфейсе управления программы появится событие безопасности.
3)Запустите web server на вашей виртуальной машине. Если она работает под Linux, используйте эту команду, и запустите web server на 8000 порту: # python -m SimpleHTTPServer.
Вовремя работы web server'а, отправьте на него атаку URL_MANY_SLASHES. Так же можно отправить атаку от внешнего устройства или с одной виртуальной машины на другую. В обоих случаях ISNP будет блокировать все атаки.
Отправить атаку URL_MANY_SLASHES легко:
В этой статье вы сможете узнать, как настроить IBM Security Network Protection (XGS5100) в основанной на Open vSwitch программно-конфигурируемой сети(SDN), и защитить-таки все ваши виртуальные активы.
Open vSwitch — это виртуальный коммутатор на основе OpenFlow, широко используемый в облачных средах.
Software-defined Networking (SDN) — это технология для развертывания облака, обеспечивающая масштабируемую и гибкую среду, подходящую для динамического характера этого самого облака.
Вы научитесь разворачивать IBM Security Network Protection (ISNP) в рамках OpenFlow с поддержкой SDN коммутатора — Open vSwitch и увидите как легко ISNP могут быть развернуты в среде SDN.

Программно-конфигурируемые сети
SDN – новый архитектурный подход, цель которого обеспечить сетевую гибкость, подходящую для динамики современной среды. Существующие сетевые технологии являются по своей сути статическими и их трудно изменить, так как небольшие сетевые изменения часто требуют существенной переконфигурации всех, или большей части коммутаторов, маршрутизаторов и межсетевых экранов. Мало того, что
процесс этот занимает много времени для администратора и не решается при помощи одного лишь бубна, он еще и несет в себе опасность получить кучу ошибок.
В архитектуре программно-конфигурируемой сети выделяется два уровня:
инфраструктурный уровень, на котором функционируют сетевые коммутаторы и каналы передачи данных, и уровень управления — набор программных средств, физически отделённых от инфраструктурного уровня, обеспечивающий реализацию механизмов управления устройствами инфраструктурного уровня.
В традиционных сетях уровень управления реализуется в устройствах передачи данных, и эта реализация зависит от поставщика.
В SDN эти уровни разделены,
управление осуществляется централизованно для всего сетевого оборудования в рамках предприятия (независимо от производителя оборудования). Эта архитектура обеспечивает простой и быстрый способ для управления потоком трафика.
Облачные среды требуют динамического распределения ресурсов. Открытые и частные облака имеют виртуальные приложения и хранилища, так что следующий логический шаг – это виртуализация сети. А почему бы и нет?!
SDN дает платформу, обеспечивающую сетевую виртуализацию, что дает возможность создать полностью динамическую среду для хранения данных, сети и приложений.
OpenFlow
SDN требует взаимодействия централизованного уровня управления с инфраструктурным уровнем (реализованным в физических устройствах). Протокол OpenFlow от Open Networking Foundation – это протокол SDN, обеспечивающий такую связь. OpenFlow позволяет детально контролировать трафик на всех коммутаторах и маршрутизаторах в сети, как
физических, так и виртуальных, независимо от поставщика программного
обеспечения.
Таким образом протокол OpenFlow устраняет необходимость конфигурирования устройства каждого поставщика в отдельности через собственный интерфейс.
Open vSwitch
Open vSwitch представляет из себя виртуальный коммутатор под лицензией Apache 2.0. Он, как правило, устанавливается на сервере для контроля трафика в гипервизоре, обеспечивая динамическую сетевую среду.
Open vSwitch поддерживает ряд протоколов для управления трафиком, в том числе NetFlow, sFlow, SPAN, RSPAN, CLI, 802.1ag и OpenFlow.
ISNP
ISNP – продукт объединяющий функции системы предотвращения вторжений и сложного контроля за приложениями.
Он дает возможность контроля над всей активностью пользователя, анализируя каждое соединение и определяя используемые приложения. В зависимости от репутации приложения ISNP может позволить или заблокировать соединение. Также ISNP может записывать информацию приложений, что может быть полезным для уточнения политики, включая пропускную способность.
Интегрированная с другими защитными функциями система предотвращения вторжений обеспечивает быструю развертку и простое администрирование.
Подготовка
Мы будем использовать 64-битный Ubuntu 12.04 LTS с поддержкой до апреля 2017. Мы устанавливали Ubuntu на «голое железо», а не на виртуальной машине. Использование «голого железа» для установки KVM гипервизора дает хорошую производительность для VM.
Сервер должен иметь как минимум три сетевых интерфейса: один для удаленного доступа, и два для подключения к
ISNP напрямую к портам защиты(как показано на Рис.1).
Рис.1

Настройка KVM гипервизора
Виртуальная машина (KVM) является инфраструктурой виртуализаци для ядра Linux, и превращает его в гипервизор.
Перед тем как заняться установкой Ubuntu, активируйте набор команд VT-d в ЦПУ, в настройках BIOS,
Рекомендуемый дистрибутив – Ubuntu 12.04 LTS.
После загрузки системы на жесткий диск, вам будет предложено выбрать дополнительные компоненты Ubuntu “из коробки”.
В разделе software selection необходимо выбрать Virtual Machine host и OpenSSH server
Рис.2

Для меня, а так же для всех неожиданно ослепших или промахнувшихся мимо нужной строки, или еще по каким либо причинам забывших выбрать Virtual Machine host, есть возможность установить необходимые компоненты KVM с помощью следующей команды: # sudo apt-get install qemu-kvm libvirt-bin.
Для завершения установки KVM гипервизора, выполните следующие действия:
- Убедитесь, что дистрибутив системы обновлен: # sudo apt-get update && apt-get dist-upgrade
- Убедитесь, что ваш процессор поддерживает KVM: # sudo kvm-ok.
- Убедитеть что в BIOS активирована функция VT-d и что ваш процессор не слишком «стар» для работы с KVM.
- Добавить пользователя в kvm group: # sudo gpasswd -a $USER kvm
- Добавить пользователя в libvirtd group:# sudo gpasswd -a $USER libvirtd
Затем, введите /etc/libvirt/qemu.conf и добавьте следующие параметры:
# sudo vi /etc/libvirt/qemu.conf
user = "root"
group = "kvm"
security_driver = "none"
cgroup_device_acl = [
"/dev/null", "/dev/full", "/dev/zero",
"/dev/random", "/dev/urandom",
"/dev/ptmx", "/dev/kvm", "/dev/kqemu",
"/dev/rtc", "/dev/hpet", "/dev/net/tun",
]
clear_emulator_capabilities = 0НЕ ЗАБУДЬТЕ РАСКОММЕНТИРОВАТЬ ВЫШЕУКАЗАННЫЕ НАСТРОЙКИ (УДАЛИТЬ # В НАЧАЛЕ КАЖДОЙ СТРОКИ)
Перезапустите libvirt-bin для загрузки и установки qemu настроек: # sudo service libvirt-bin restart.
При желании вы можете установить virt-manager : # sudo apt-get install virt-manager. Утверждается, что у него удобный интерфейс для настройки виртуальных машин.
Настройка Open vSwitch
Чтобы настроить Open vSwitch, вам придется установите все необходимые компоненты Open vSwitch (Подойдет Open vSwitch 1.4.0 ):
# sudo apt-get install openvswitch-controller openvswitch-switch openvswitch-datapath-source openvswitch-datapath-dkmsПримечание: при установке этих пакетов на ядре 3.8 вы можете столкнуться некоторыми проблемами, но сотрудники Ubuntu усердно трудятся над их решениям, пока я пишу статью. А теперь о приятном – в ядре 3.8 уже есть нативный openvswitch module, по этому нет необходимости самим собирать его.
Как только openvswitch module будет загружен, так сразу ваша система будет готова к использованию.
Ах да, убедитесь что вы все таки загрузили openvswitch module и вам это не приснилось: # lsmod | grep openvswitch . А если вы вдруг захотите проверить запущены ли ovsdb-server и ovs-vswitchd, то используйте эту команду: # sudo service openvswitch-switch status
Вы должны увидеть это:
ovsdb-server is running with pid xxxx
ovs-vswitchd is running with pid yyyyКонфигурирование Open vSwitch
Следующий шаг демонстрирует как сконфигурировать Open vSwitch и использовать интерфейс eth0 как порт uplink
После этого Виртуальные Машины подключатся к коммутатору и получат доступ к сети.
Чтобы еще раз убедиться в том, что вы «умничка», ваш Open vSwitch готов к использованию и вы все сделали правильно, выполните эти команды:
- Убедитесь в том, что вы загрузили Open vSwitch module: # lsmod | grep openvswitch.
Вы должны увидеть что-то, похожее на это: # openvswitch 47849 0 - Проверьте статус всех сервисов Open vSwitch: # sudo service openvswitch-switch status .
Вы должны увидеть это:
ovsdb-server is running with pid xxxx
ovs-vswitchd is running with pid yyyyУбедительная просьба заняться конфигурированием после того, как вы убедитесь что все сервисы Open vSwitch работают корректно.
Сбрасываем настройки eth0:
# sudo ifconfig eth0 0Создаем новый vSwitch:
# sudo ovs-vsctl add-br ovs-internalДобавляем eth0 на ovs-internal:
# sudo ovs-vsctl add-port ovs-internal eth0Поднимаем ovs-internal:
# sudo ifconfig ovs-internal upУстанавливаем IP адрес для ovs-internal:
Статический IP:
# sudo ifconfig ovs-internal <ip> <netmask>
# sudo route add default gw <gw_ip>DHCP:
# sudo dhclient ovs-internalДобавляем eth1 и eth2 к ovs-internal. Вводим команды в указанном порядке:
# sudo ovs-vsctl add-port ovs-internal eth1
# sudo ovs-ofctl mod-port ovs-internal eth1 down
# sudo ovs-ofctl mod-port ovs-internal eth1 noflood
# sudo ovs-vsctl add-port ovs-internal eth2
# sudo ovs-ofctl mod-port ovs-internal eth2 down
# sudo ovs-ofctl mod-port ovs-internal eth2 nofloodПосле введения этих команд происходит деактивация сетевых интерфейсов eth1 и eth2 и устанавка на них опции noflood.
Необходимо соблюдать порядок ввода команд, не то получите loop. Эти 2 порта заработают, когда устройство ISNP готово и кабели воткнуты в eth1 и eth2.
После того, как установка Open vSwitch будет завершена вы можете воспользоваться ovs-vsctl и увидеть статус ваших коммутаторов.
# sudo ovs-vsctl show
ed1f5e9a-8c2e-4a1e-9fe8-73740f57589c
Bridge ovs-internal
Port ovs-internal
Interface ovs-internal
type: internal
Port "eth2"
Interface "eth2"
Port "eth1"
Interface "eth1"
Port "eth0"
Interface "eth0"
ovs_version: "1.4.0+build0"Если вы не хотите каждый раз настраивать Open vSwitch зайдите /etc/network/interfaces и добавьте «постоянные» настройки
Для статической конфигурации IP, необходимо изменить настройки так, чтобы было похоже на это:
# The loopback network interface
auto lo
iface lo inet loopback
# The uplink on ovs-internal
auto eth0
iface eth0 inet static
address 0.0.0.0
# The interface for connecting to the protection ports on ISNP
auto eth1
iface eth1 inet static
address 0.0.0.0
# The interface for connecting to the protection ports on ISNP
auto eth2
iface eth2 inet static
address 0.0.0.0
# The Open vSwitch setting
auto ovs-internal
iface ovs-internal inet static
address 10.40.28.1
netmask 255.255.128.0
network 10.40.0.0
broadcast 10.40.127.255
gateway 10.40.0.1
dns-nameservers 10.40.1.1А для того чтобы сконфигурировать DHCP, настройки должны быть похожи на это:
# The loopback network interface
auto lo
iface lo inet loopback
# The uplink on ovs-internal
auto eth0
iface eth0 inet static
address 0.0.0.0
# The interface for connecting to the protection ports on ISNP
auto eth1
iface eth1 inet static
address 0.0.0.0
# The interface for connecting to the protection ports on ISNP
auto eth2
iface eth2 inet static
address 0.0.0.0
# The primary network interface
auto ovs-internal
iface ovs-internal inet dhcpВажно установить noflood на eth1 и eth2. В /etc/network/interfaces делать это не желательно, поэтому вам будет необходимо ввести следующие команды в /etc/rc.local:
# sudo vi /etc/rc.local
ovs-ofctl mod-port ovs-internal eth1 noflood
ovs-ofctl mod-port ovs-internal eth2 nofloodНастройка ISNP
Настройте свой ISNP и подключите eth1 и eth2 к портам устройства (как показано на рисунке 1 ).
Когда установка завершиться, вы сможете войти в интерфейс и увидеть панель управления ISNP.
Рис.3

Для этой статьи ISNP использовался как IPS. Мы использовали стоявшую по умолчанию X-Force IPS, а не сетевую политику контроля пользователей и приложений. В итоге было активировано только правило «any any». Остальные правила, указанные в начальных настройках поставляются вместе с XGS5100(версия 5.1)
Рис.4

После настройки ISNP подключите кабели и поднимите eth1 и eth2 порты на ovs-internal:
# sudo ovs-ofctl mod-port ovs-internal eth1 up
# sudo ovs-ofctl mod-port ovs-internal eth2 upПерепроверьте правильно ли вы установили noflood на eth1 и eth2, потому что если нет, то при подключении кабелей получите loop.
Создание первой виртуальной машины и подключение ее к ovs-internal
Для начала вам необходимо приготовить скрипт для подключения вашей виртуальной NIC на вашей виртуальной машине к ovs-internal.
Скопируйте этот код в /etc/ovs-ifup:
# sudo vi /etc/ovs-ifup
#!/bin/sh
switch='ovs-internal'
/sbin/ifconfig $1 0.0.0.0 up
ovs-vsctl add-port ${switch} $1Добавьте разрешение на исполнение скрипта: # sudo chmod +x /etc/ovs-ifup.
Создание новой виртуальной машины
Для создания виртуальной машины воспользуйтесь virt-manager. Так как здесь использовался Ubuntu 12.04 server и мы не установили X-сервер, то мы не сможем запустить какую либо программу с GUI.
Но если вдруг вы решили использовать Desktop Edition, то проблема будет решена и вы можете получить доступ к virt-manager напрямую.
Для запуска virt-manager на вашей KVM, используйте X forwarding(для просмотра GUI программ на вашем локальном сервере)
Если вы работаете под Linux, то для соединения с удаленным KVM необходимо запустить команду активирующую X forwarding. (Соединение X forwarding с сервером по протоколу SSH): # ssh -X user@<server_ip>.>.
Вместо eth0 вам необходимо получить IP-адрес вашего сервера от ovs-internal : # ifconfig ovs-internal>.
После входа на удаленный KVM, запустите virt-manager: # virt-manager.
Если все правильно, то отобразится GUI программы.
Рис.5

Теперь создаем первую виртуальную машину.
Рис.6

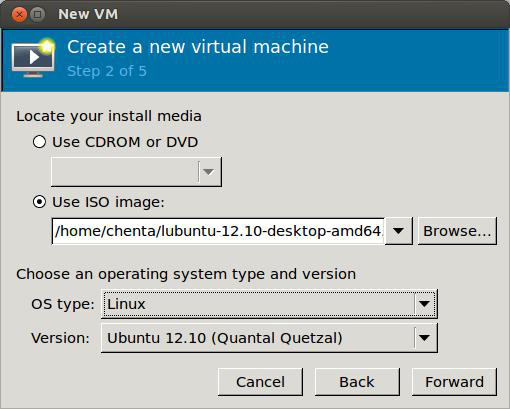
Рис.7

У нее должен быть хотя бы один vNIC (Virtualized Network Interface)
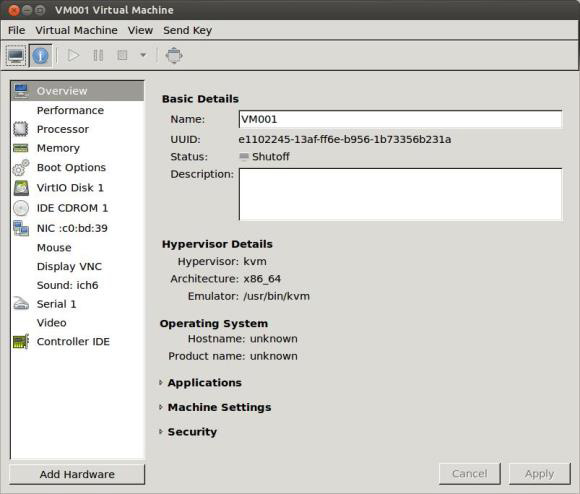
Рис.8

vNIC будут отконфигурированы позже, а пока закройте созданную виртуальную машину и вручную измените ее XML-файл:Edit /etc/libvirt/qemu/.xml.
Изначально настройки XML-файла должны выглядеть так:
# sudo vi /etc/libvirt/qemu/<VM NAME>.xml
<interface type='bridge'>
<mac address='xx:xx:xx:xx:xx:xx'/>
<source bridge='xxxx'/>
<model type='virtio'/>
<address type='pci' domain='0x0000' bus='0x00'
slot='0x03' function='0x0'/>
</interface>Измените настройки XML-файла, чтобы он выглядел так:
<interface type='ethernet'>
<mac address='xx:xx:xx:xx:xx:xx'/>
<script path='/etc/ovs-ifup'/>
<model type='virtio'/>
<address type='pci' domain='0x0000' bus='0x00'
slot='0x03' function='0x0'/>
</interface>Отдайте команду KVM загрузить обновленный XML-файл: # sudo virsh define /etc/libvirt/qemu/.xml.
Все! «Властвуйте и разделяйте» на созданной вами виртуальной машине.
Выполнив следующие команды вы должны увидеть созданный порт на ovs-internal.
# sudo ovs-vsctl show
# sudo ovs-ofctl show ovs-internalПопробуйте установить на вашу виртуальную машину любую операционную систему и попытайтесь подключиться к сети.
Когда ваша виртуальная машина соединена с Open vSwitch на ней должны работать сеть(в режиме моста) и DHCP сервер. Если DHCP сервер не доступен, то вам придется назначить IP адрес виртуальной машине вручную.
Из-за ошибки в Libvirt, ovs-ifdown скрипт не указан в файле описания. Необходимо выключить виртуальную машину и отключить tap (Ethernet) устройство от коммутатора. Если этого не сделать, то сообщение об ошибке будет появляться и при последующих запусках виртуальной машины.
Рис.9

Чтобы отключить tap устройство от ovs-internal необходимо ввести эту команду: # sudo ovs-vsctl del-port ovs-internal tapN.
из сообщения об ошибке мы можем узнать какое устройство отключено от коммутатора. (Рис.9)
Защита виртуальной машины от внешнего трафика
Теперь необходимо «обучить» ovs-internal проверке пакетов, при передаче трафика в ISNP. Используйте команду ovs-ofctl для установки правил SDN на ovs-internal. Структура правил при работе с коммутатором определяется стандартом OpenFlow. Повторите то же самое для защиты других виртуальных машин.
Если вы установили не верные правила, ваша виртуальная машина не сможет пользоваться сетью. Чтобы восстановить подключение к сети необходимо сбросить настройки коммутатора используя следующие команды:
# sudo ovs-ofctl del-flows ovs-internal
# sudo ovs-ofctl add-flow ovs-internal action=normalВы должны знать два атрибута с первой виртуальной машины: МАС-адрес и номер порта через который ваша Виртуальная машина соединяется с ovs-internal.
Посмотреть МАС-адрес вашей виртуальной NIC можно здесь:
/etc/libvirt/qemu/.xml:
#sudo vi /etc/libvirt/qemu/<VM NAME>.xml
<interface type='ethernet'>
...
<mac address='xx:xx:xx:xx:xx:xx'/>
...
</interface>Так же можно посмотреть МАС-адрес, присваивающийся каждому сетевому устройству, непосредственно на самой виртуальной машине.
Теперь вам нужен номер порта через который ваша Виртуальная машина соединяется с ovs-internal. Чтобы получить статус порта на ovs-internal необходимо запустить следующую команду: # sudo ovs-ofctl show ovs-internal.
Вывод команды должен выглядеть следующим образом:
OFPT_FEATURES_REPLY (xid=0x1): ver:0x1, dpid:0000e41f136c4952
n_tables:255, n_buffers:256
features: capabilities:0xc7, actions:0xfff
1(eth0): addr:e4:1f:13:6c:49:52
config: 0
state: 0
current: 1GB-FD COPPER AUTO_NEG
advertised: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD AUTO_NEG
supported: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD COPPER AUTO_NEG
2(eth1): addr:e4:1f:13:6c:aa:56
config: NO_FLOOD
state: 0
current: 1GB-FD COPPER AUTO_NEG
advertised: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD AUTO_NEG
supported: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD COPPER AUTO_NEG
3(eth2): addr:e4:1f:13:6c:ab:57
config: NO_FLOOD
state: 0
current: 1GB-FD COPPER AUTO_NEG
advertised: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD AUTO_NEG
supported: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD COPPER AUTO_NEG
4(tap0): addr:be:cc:7b:8b:c0:04
config: 0
state: 0
current: 10MB-FD COPPER
LOCAL(ovs-internal): addr:e4:1f:13:6c:49:52
config: 0
state: 0Цифры (от 1 до 4) это номер порта, следом в скобках-название подключенного к порту устройства.
Каждое vNIC на виртуальной машине отображается как tap устройство гипервизора. Таким образом, мы можем видеть, что первая виртуальная машина подключена к 4 порту на ovs-internal, eth2 ко 2 порту, и eth3 к 3 порту. Все эти значения вы увидите в правилах управления коммутатором.
Обратите внимание, что номер порта на коммутаторе может быть изменен после перезагрузки сервера.
Необходимо использовать верный номер порта в последующих правилах управления ovs-internal, в противном случае сетевой трафик не будет проходить через ISNP устройства…
Примечание: eth0 не всегда будет находится на первом порту.
Предположим, что MAC-адрес первой Виртуальной Машины 52: 54: 00: AA: BB: CC.
Установите новые правила для ovs-internal.
Rule 01: # sudo ovs-ofctl del-flows ovs-internal
Rule 02: # sudo ovs-ofctl add-flow ovs-internal
priority=100,in_port=1,dl_dst=52:54:00:ac:bb:cc,idle_timeout=0,action=output:2
Rule 03: # sudo ovs-ofctl add-flow ovs-internal
priority=100,in_port=3,dl_dst=52:54:00:ac:bb:cc,idle_timeout=0,action=output:4
Rule 04: # sudo ovs-ofctl add-flow ovs-internal
priority=100,in_port=4,idle_timeout=0,action=output:3
Rule 05: # sudo ovs-ofctl add-flow ovs-internal
priority=0,action=normalПравила по правилам
Rule 01: Flush every rule on ovs-internal
Rule 02: If the flow is sent from the uplink (eth0 @ port #1) and the destination MAC is
“52:54:00:aa:bb:cc” then forward the flow to eth1@port#2.
Rule 03: After ISNP inspected the flow, it will be forwarded to eth2@port#3. Therefore,
if the flow is sent from port#3 and the destination MAC is “52:54:00:aa:bb:cc”
then it should be forward the port that the first VM is connected to (port#4).
Rule 04: Forward every packets sent from the first VM (port#4) to eth2 (port #3).
Rule 05: It is the default rule to handle the broadcast/multicast traffic. This rule has
the lowest priority.Синие линии, на рис. 10 демонстрируют как как коммутатор пересылает трафик, передаваемый от внешнего компьютера на ISNP, а затем на первую виртуальную машину.
Рис.10

С помощью этой команды вы можете сбросить все текущие правила на ovs-internal и посмотреть как много пакетов «убило» каждое правило: # sudo ovs-ofctl dump-flows ovs-internal.
Вывод должен выглядеть примерно так:
NXST_FLOW reply (0x4):
cookie=0x0, duration=4345.083s, table=0, n_packets=4637, n_bytes=441598,
priority=100,in_port=4 actions=output:3
cookie=0x0, duration=4399.466s, table=0, n_packets=4618, n_bytes=449256,
priority=100,in_port=1,dl_dst=52:54:00:aa:bb:cc actions=output:2
cookie=0x0, duration=4363.898s, table=0, n_packets=4618, n_bytes=449256,
priority=100,in_port=3,dl_dst=52:54:00:aa:bb:cc actions=output:4
cookie=0x0, duration=4324.14s, table=0, n_packets=24095, n_bytes=1916023,
priority=0 actions=NORMALТеперь вы можете проверить работу ISNP и запустить на первой виртуальной машине тесты на проникновение.
В разделе ,«Verify that the ISNP device is protecting your virtual machines» есть несколько простых тестов, для проверки ISNP защиты вашей виртуальной машины
Создание второй виртуальной машины и подключение ее к Open vSwitch
Вторую виртуальную машину вы можете создать путем клонирования первой, используя virt-manager, или вручную, как вы делали ранее
Не забудьте изменить XML-файл, чтобы виртуальная машина автоматически подключаться к ovs-internal
Защита Виртуальной Машины от внутреннего трафика
Чтобы получить номер порта, используемого второй Виртуальной Машиной, снова запустите ovs-ofctl команду:# sudo ovs-ofctl show ovs-internal.
Результат будет выглядеть примерно так:
OFPT_FEATURES_REPLY (xid=0x1): ver:0x1, dpid:0000e41f136c4952
n_tables:255, n_buffers:256
features: capabilities:0xc7, actions:0xfff
1(eth0): addr:e4:1f:13:6c:49:52
config: 0
state: 0
current: 1GB-FD COPPER AUTO_NEG
advertised: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD AUTO_NEG
supported: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD COPPER AUTO_NEG
2(eth1): addr:e4:1f:13:6c:aa:56
config: NO_FLOOD
state: 0
current: 1GB-FD COPPER AUTO_NEG
advertised: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD AUTO_NEG
supported: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD COPPER AUTO_NEG
3(eth2): addr:e4:1f:13:6c:ab:57
config: NO_FLOOD
state: 0
current: 1GB-FD COPPER AUTO_NEG
advertised: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD AUTO_NEG
supported: 10MB-HD 10MB-FD 100MB-HD 100MB-FD 1GB-FD COPPER AUTO_NEG
4(tap0): addr:be:cc:7b:8b:c0:04
config: 0
state: 0
current: 10MB-FD COPPER
5(tap1): addr:be:cc:7b:8b:c0:05
config: 0
state: 0
current: 10MB-FD COPPER
LOCAL(ovs-internal): addr:e4:1f:13:6c:49:52
config: 0
state: 0Здесь мы видим что новое tap устройство подключено к ovs-internal через пятый порт.
Предположим, что MAC-адрес второй Виртуальной Машины 52: 54: 00: AA: CC: DD. Необходимо установить следующие правила для ovs-internal, чтобы защитить его от внешнего трафика и от трафика между Виртуальными машинами.
Rule 06: # sudo ovs-ofctl add-flow ovs-internal
priority=100,in_port=1,dl_dst=52:54:00:ac:cc:dd,idle_timeout=0,action=output:2
Rule 07: # sudo ovs-ofctl add-flow ovs-internal
priority=100,in_port=3,dl_dst=52:54:00:ac:cc:dd,idle_timeout=0,action=output:5
Rule 08: # sudo ovs-ofctl add-flow ovs-internal
priority=100,in_port=5,idle_timeout=0,action=output:3
Rule 09: sudo ovs-ofctl add-flow ovs-internal
priority=100,in_port=2,dl_dst=52:54:00:ac:bb:cc,idle_timeout=0,action=output:4
Rule 10: sudo ovs-ofctl add-flow ovs-internal
priority=100,in_port=2,dl_dst=52:54:00:ac:cc:dd,idle_timeout=0,action=output:5Правила по правилам
Rule 06–08: These rules protect the second VM from the external traffic.
Rule 09: Because you must take care of the inter-vm traffic now, you need to tell the
switch how to forward the inter-vm traffic after ISNP inspects it. This rule
says that after ISNP returns the traffic — and if the destination is to the
first VM — the traffic should be forwarded to port #4.
Rule 10: After ISNP inspects the traffic, it will be forwarded to port #2. This rule
forwards the traffic to port #5 if the destination is the second VM.Красные линии на рисунке 11 отображают новые правила, установленные для коммутатора(защищающие трафик между двумя виртуальными машинами).
Рис.11

Удостоверьтесь что все правила, установленные для ovs-internal корректны: # sudo ovs-ofctl dump-flows ovs-internal.
Здесь вы так же можете проверить работу ISNP, запустив тестирование на проникновение из одной виртуальной машины на другую.
ISNP-защита ваших виртуальных машин (несколько простых тестов)
1)Самый простой способ убедиться, что сетевой трафик пошел через ISNP — это использовать Network Graphs в интерфейсе управления ISNP. Перед тем как Network Graphs начнут проверку необходимо отправить часть трафика на виртуальные машины.
Перед проверкой мы имеем возможность выбрать интересующий нас график.
Рис.12

Рекомендовано использовать"Detail by User". В этом случае, если IP-адреса ваших виртуальных машин появятся в сетевой статистике, то график будет похож на то что мы видим на Рис.13
Рис.13

2)Вы можете послать на ваши виртуальные машины безвредную атаку и посмотреть блокирует ли их ваш ISNP.
При корректной работе ISNP атаки будут блокированы, а в интерфейсе управления программы появится событие безопасности.
3)Запустите web server на вашей виртуальной машине. Если она работает под Linux, используйте эту команду, и запустите web server на 8000 порту: # python -m SimpleHTTPServer.
Вовремя работы web server'а, отправьте на него атаку URL_MANY_SLASHES. Так же можно отправить атаку от внешнего устройства или с одной виртуальной машины на другую. В обоих случаях ISNP будет блокировать все атаки.
Отправить атаку URL_MANY_SLASHES легко:
- Чтобы инициировать событие, введите более чем 500 слешей в запросе HTTP
- Откройте веб-браузер, и войдите в этот URL:http://:8000///////////////.....////////////////////////
Чтобы отправить атаку URL_MANY_SLASHES так же можно использовать команду:
# wget http://10.40.25.10:8000/`python -c "print '/'*500"`
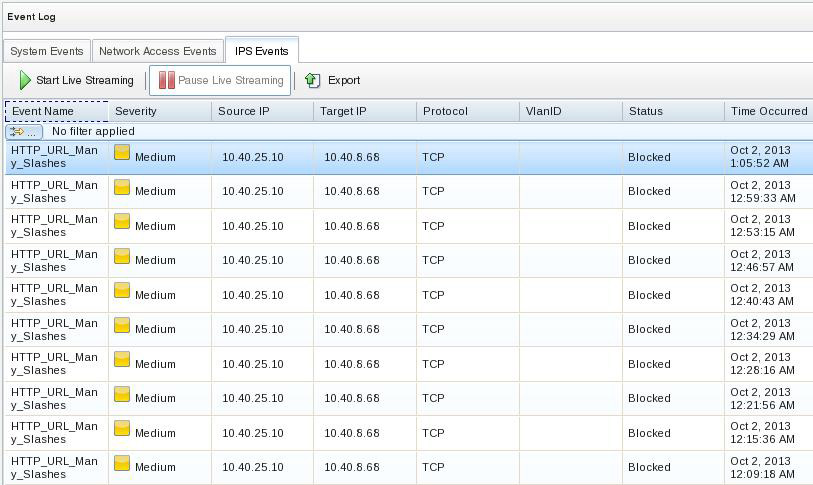
После отправки атаки проверьте события безопасности в Журнале событий (Event Log view).
Выберите IPS События (IPS Events) и вы сможете увидеть все заблокированные ISNP события безопасности. (Рис.14)
Рис.14
 .
.
 .
.