Красота растений привлекала внимание математиков веками. Активнее всего изучались интересные геометрические свойства растений, такие как симметрия листьев относительно центральной оси, радиальная симметрия цветов, и спиральное расположение семечек в шишках. «Красота связана с симметрией» (H. Weyl. Symmetry). Во время роста живых организмов, особенно растений, можно четко видеть регулярно повторяющиеся многоклеточные структуры. В случае составных листьев, например, маленькие листочки, которые являются частью большого взрослого листа, имеют ту же форму, что весь лист имел на раннем этапе формирования.
В 1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов. Эта модель получила название Lindenmayer System, или просто L-System.
Для тех, кто в теме и не хочет все читать целиком, проскрольте вниз, есть вопрос.
Я буду сокращать L-System до L в тексте.
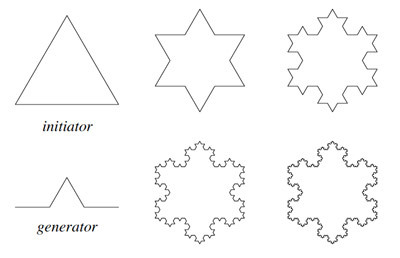
Основная идея L — постоянная перезапись (rewriting) элементов строки. О чем это? Вкратце, rewriting — это способ получения сложных объектов путем замены частей простого начального объекта по некоторым правилам. Классическим примером является снежинка. На рисунке initiator — это начальный объект, грани которого заменяются на generator. Далее с новым объектом проделывается то же самое. В данном случае обычный фрактал.
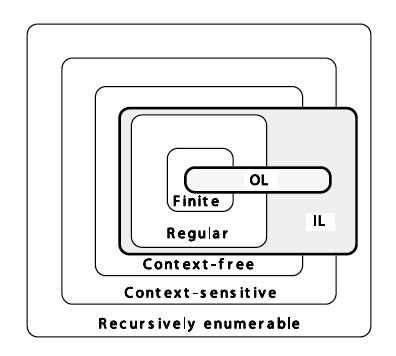
Возвращаясь к L и проводя аналогию с фракталами, можно сказать, что L оперирует со строкой символов по специальным правилам, начиная с первоначальной простой аксиомы. Люди, знакомые с понятием грамматики, сразу заметят, что по сути L ей и является. Но фундаментальное отличие L от формальных грамматик состоит в том, что правила применяются одновременно ко всей строке, к каждому символу, плюс, нет понятий терминальных и нетерминальных символов. То есть «вывод» по этой грамматике может продолжаться бесконечно. Одновременность применения правил очень быстро становится понятна, если учесть откуда пришла эта модель. В биологии каждая клетка растет, делится и развивается параллельно во времени. На следующей картинке видно соотношение между контекстносвободными (OL), контекстнозависимыми (IL) L и другими формальными грамматиками в иерархии Хомского.
Также, как и в классификации Хомского, L имеют и свою классификацию от простых до сложных и мощных.
Самым простым примером являются детерминированные контекстносвободные L или сокращенно DOL. Я не люблю формальные определения грамматик, так что скажу просто своими словами. Есть некоторый набор символов — алфавит. Этим алфавитом записывается строка, с которой работает L. Есть аксиома — первоначальная строка из одной или более буквы и набор правил вида a → ab. Во время каждой итерации алгоритма, применяя правило к букве из текущей строки, она (буква) заменяется на набор букв справа от стрелки. Проще рассмотреть конкретный пример развития многоклеточного организма Anabaena catenula, который изучал Линденмайер, когда он предложил модель L.
Пусть наш алфавит состоит из следующих символов, каждый из которых обозначает некоторую клетку: al ar bl br.
Аксиома состоит из одного символа.
ω: ar
И 4 правила.
p1: ar → albr
p2: al → blar
p3: br → ar
p4: bl → al
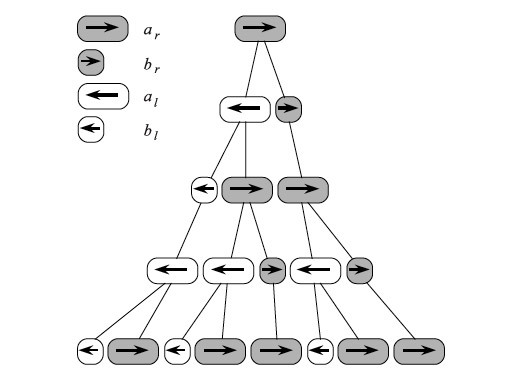
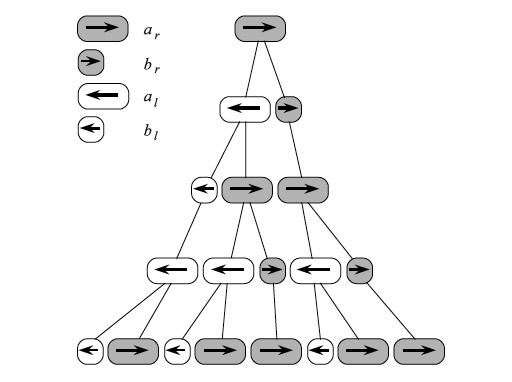
Правила говорят какие символы меняются на какие в процессе роста организма. На картинке видно как применяя правила мы наблюдаем «деление» клеток и развитие.
Пока мы видели как нарисовать одномерную бактерию, но с помощью известного детского языка программирования LOGO, в котором предлагается управлять черепашкой и рисовать фигуры на экране, можно будет уже рисовать двумерные и трехмерные фракталы и повторяющиеся структуры. Как? Все просто. Берем алфавит, в котором каждый символ означает некоторую команду для двумерной или трехмерной черепашки:
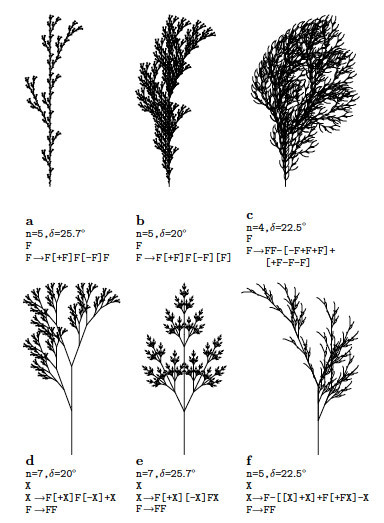
Эти команды используют дефолтные значения угла поворота δ, длины шага и базисные векторы двумерного и трехмерного пространства. Примеры двумерных фракталов и порождающих их L можно увидеть на следующей картинке.

Все, что было до этого является, в общем-то, непрерывными кривыми. Разумеется, таким образом весьма трудно смоделировать растения с их ветвящейся топологией. Для этого в алфавит были добавлены символы [ и ], которые обозначают начало и конец ветвления соответственно. Когда черепашка встречает символ [, ее текущее состояние пишется в стек и вытаскивается оттуда при встрече символа ].
Уже такой простой грамматикой можно сгенерировать довольно интересные двумерные и трехмерные объекты похожие на деревья.
Разумеется, наука не стояла на месте, и сейчас мы имеем солидную иерархию L начиная с простых DOL рассмотренных ранее.
Стохастические L.
Стохастические L добавляют возможность задания вероятности выполнения того или иного правила, и в общем случае не являются детерминированными, ибо разные правила могут иметь один и тот же символ слева. Это вносит некоторый элемент случайности в получающиеся структуры.
Контекстнозависимые L.
Также, как и контекстнозависимость в формальных граматиках, в L синтаксис правил усложняется и принимает во внимание окружение заменяемого символа.
Парамметрические L.
К каждому символу добавляется параметр-переменная (возможно не одна), которая позволяет, например указывать величину угла поворота для + и -, длину шага и толщину линии, проверять условия для применения правила, считать количество итераций и передавать «сигналы» вперед и назад. Пример парамметрической L.
Парамметрические контекстнозависимые L позволяют моделировать рост многоклеточных организмов и растений с учетом биохимических процессов и окружающей среды. Например, наша старая знакомая Anabaena catenula в более сложной форме. Пример из книжки [1].
Как написано в книге, данная бактерия состоит из двух видов клеток: вегетативные клетки и гетероцисты. Обычно, вегетативные клетки делятся на две подобные вегетативные клетки. Однако, в некоторых случаях вегетативные клетки превращаются в гетероцистов. Их распределение следует хорошо наблюдаемому шаблону, в котором соседние гетероцисты разделены примерно одинаковым числом вегетативных клеток. Но как же организм поддерживает постоянное расстояние между гетероцистами во время роста? Предложенная модель описывает этот феномен с точки зрения биологии. Предполагается, что расположение гетероцистов регулируется соединениями азота, производимые этими клетками, которые передаются в другие клетки организма и потребляются в вегетативных клетках. Если содержание этих соединений в молодй вегетативной клетке падает ниже определенного уровня, эта клетка превращается в гетероцист.
L-System ниже моделирует рост бактерии с учетом вышесказанного.
#define присваивает значения константам используемым в L.
#include загружает форму гетероциста, в данном случае круг.
Клетки представлены модулем F(s, t, c), где s — длина клетки, t — тип клетки (0 — гетероцист, 1 и 2 — вегетативные клетки), а c — концентрация азота.

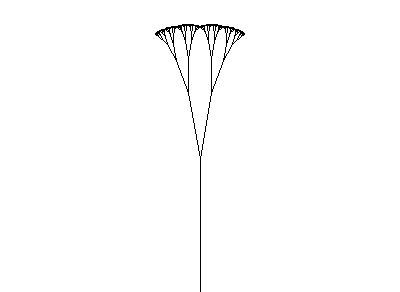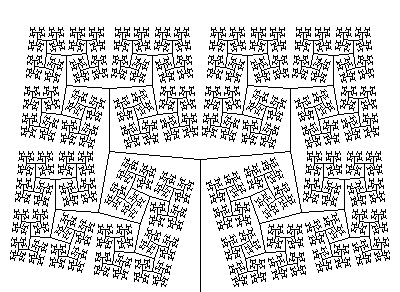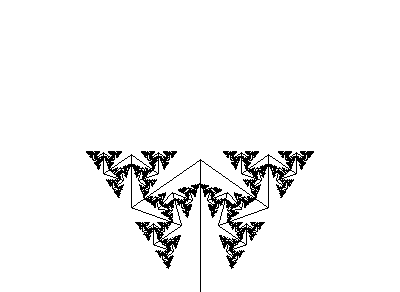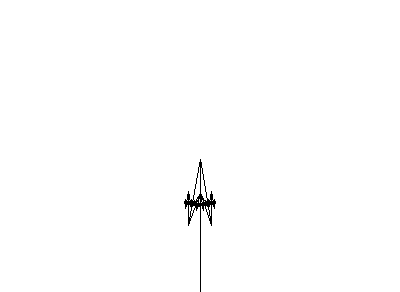
Вот, например, недавняя гипножаба, покорившая интернет, по сути является комбинацией простейших L.
Это всего лишь поверхностное описание теории и небольшие примеры применения на практике. Что ждет любопытного исследователя дальше?




Еще в конце 80х L использовались для визуализации моделей растений. Сейчас возможности компьютеров ушли далеко вперед. Многие игры и инструменты 3d моделирования используют процедурную генерацию контента, в том числе и L-Systems. Как видите, из набора простых правил можно получить огромное количество разных растений и засадить ими целые поля.
Из редакторов я сам пользуюсь L в Houdini, слышал, что есть плагины и для других пакетов. Так называемая Виртуальная Лаборатория позволяет экспериментировать и анимировать L.
Методы использования грамматик также используются в так называемых Shape Grammars, но об этом потом.
Некоторые посты в интернете.
http://avalter.blogspot.com/2009/08/2d-l.html
Вообще говоря, единственная доступная книга — это The Algorithmic Beauty of Plants. Также, по интернету разбросаны старые рандомные статьи. Более-менее новые можно найти на springerlink.com за кучу денег или в институтской библиотеке забесплатно.
Что сказать, материала довольно маловато.
Я сам имею ровно никакое отношение к биологии, а являюсь Магистром Математики с небольшими невиными увлечениями. Но мне чрезвычайно нравится идея L-Systems. Простота с огромными возможностями. Когда-то давно я задумывался как же так в ДНК содержится полная информация обо мне. Как же можно в каждую клетку впихнуть всю информацию обо всех клетках? А никак, можно сказать, теория L открыла мне глаза! У меня в ДНК написано не как я выгляжу, а как меня собрать (общими словами). Что-то похожее на набор правил в L, только относящееся к синтезу протеинов.
Простая модель так четко описывает нашу с вами жизнь.
Дальше больше — превращаем правила в «ДНК» и генетическим алгоритмом выращиваем виртуальных многоклеточных.
Мне бы хотелось найти людей, которые тоже заинтересованы в научной составляющей L, поделиться материалами и статьями. Так уж получилось, что я сейчас работаю над апгрейженной концепцией L-Systems, но не имею возможности просмотреть что писалось по этой теме за последние пять лет. Не хочется изобретать велосипед.
Связаться с автором КНИГИ не удалось, автоответчик говорит, что он уехал на шабаш до января (8
Также, я ищу информацию по Shape Grammars для 3d моделирования. Есть задача генерировать из параметров космические корабли, ну знаете такие огромные штуковины с кучей мелких деталей — идеальные кандидаты для SG. Неужели придется писать плагин для Houdini на Python?
В 1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов. Эта модель получила название Lindenmayer System, или просто L-System.
Для тех, кто в теме и не хочет все читать целиком, проскрольте вниз, есть вопрос.
Я буду сокращать L-System до L в тексте.
Rewriting.
Основная идея L — постоянная перезапись (rewriting) элементов строки. О чем это? Вкратце, rewriting — это способ получения сложных объектов путем замены частей простого начального объекта по некоторым правилам. Классическим примером является снежинка. На рисунке initiator — это начальный объект, грани которого заменяются на generator. Далее с новым объектом проделывается то же самое. В данном случае обычный фрактал.

Возвращаясь к L и проводя аналогию с фракталами, можно сказать, что L оперирует со строкой символов по специальным правилам, начиная с первоначальной простой аксиомы. Люди, знакомые с понятием грамматики, сразу заметят, что по сути L ей и является. Но фундаментальное отличие L от формальных грамматик состоит в том, что правила применяются одновременно ко всей строке, к каждому символу, плюс, нет понятий терминальных и нетерминальных символов. То есть «вывод» по этой грамматике может продолжаться бесконечно. Одновременность применения правил очень быстро становится понятна, если учесть откуда пришла эта модель. В биологии каждая клетка растет, делится и развивается параллельно во времени. На следующей картинке видно соотношение между контекстносвободными (OL), контекстнозависимыми (IL) L и другими формальными грамматиками в иерархии Хомского.

Самые простые L-Systems.
Также, как и в классификации Хомского, L имеют и свою классификацию от простых до сложных и мощных.
Самым простым примером являются детерминированные контекстносвободные L или сокращенно DOL. Я не люблю формальные определения грамматик, так что скажу просто своими словами. Есть некоторый набор символов — алфавит. Этим алфавитом записывается строка, с которой работает L. Есть аксиома — первоначальная строка из одной или более буквы и набор правил вида a → ab. Во время каждой итерации алгоритма, применяя правило к букве из текущей строки, она (буква) заменяется на набор букв справа от стрелки. Проще рассмотреть конкретный пример развития многоклеточного организма Anabaena catenula, который изучал Линденмайер, когда он предложил модель L.
Пусть наш алфавит состоит из следующих символов, каждый из которых обозначает некоторую клетку: al ar bl br.
Аксиома состоит из одного символа.
ω: ar
И 4 правила.
p1: ar → albr
p2: al → blar
p3: br → ar
p4: bl → al
Правила говорят какие символы меняются на какие в процессе роста организма. На картинке видно как применяя правила мы наблюдаем «деление» клеток и развитие.
Черепашья интерпретация строк.
Пока мы видели как нарисовать одномерную бактерию, но с помощью известного детского языка программирования LOGO, в котором предлагается управлять черепашкой и рисовать фигуры на экране, можно будет уже рисовать двумерные и трехмерные фракталы и повторяющиеся структуры. Как? Все просто. Берем алфавит, в котором каждый символ означает некоторую команду для двумерной или трехмерной черепашки:
- F — продвинуться вперед и нарисовать линию
- f — продвинуться вперед ничего не рисуя
- + — повернуть влево
- — — повернуть вправо
- & — повернуть вниз
- ^ — повернуть вверх
- \ — наклониться влево
- / — наклониться вправо
- | — развернуться на 180 градусов
Эти команды используют дефолтные значения угла поворота δ, длины шага и базисные векторы двумерного и трехмерного пространства. Примеры двумерных фракталов и порождающих их L можно увидеть на следующей картинке.

Растения и ветвящиеся структуры.
Все, что было до этого является, в общем-то, непрерывными кривыми. Разумеется, таким образом весьма трудно смоделировать растения с их ветвящейся топологией. Для этого в алфавит были добавлены символы [ и ], которые обозначают начало и конец ветвления соответственно. Когда черепашка встречает символ [, ее текущее состояние пишется в стек и вытаскивается оттуда при встрече символа ].
Уже такой простой грамматикой можно сгенерировать довольно интересные двумерные и трехмерные объекты похожие на деревья.

Более сложные грамматики.
Разумеется, наука не стояла на месте, и сейчас мы имеем солидную иерархию L начиная с простых DOL рассмотренных ранее.
Стохастические L.
Стохастические L добавляют возможность задания вероятности выполнения того или иного правила, и в общем случае не являются детерминированными, ибо разные правила могут иметь один и тот же символ слева. Это вносит некоторый элемент случайности в получающиеся структуры.
Контекстнозависимые L.
Также, как и контекстнозависимость в формальных граматиках, в L синтаксис правил усложняется и принимает во внимание окружение заменяемого символа.
Парамметрические L.
К каждому символу добавляется параметр-переменная (возможно не одна), которая позволяет, например указывать величину угла поворота для + и -, длину шага и толщину линии, проверять условия для применения правила, считать количество итераций и передавать «сигналы» вперед и назад. Пример парамметрической L.
ω : B(2)A(4, 4)
p1 : A(x, y) :y <= 3 → A(x ∗ 2, x + y)
p2 : A(x, y) :y > 3 → B(x)A(x/y, 0)
p3 : B(x) :x < 1 → C
p4 : B(x) :x >= 1 → B(x − 1)Парамметрические контекстнозависимые L позволяют моделировать рост многоклеточных организмов и растений с учетом биохимических процессов и окружающей среды. Например, наша старая знакомая Anabaena catenula в более сложной форме. Пример из книжки [1].
Как написано в книге, данная бактерия состоит из двух видов клеток: вегетативные клетки и гетероцисты. Обычно, вегетативные клетки делятся на две подобные вегетативные клетки. Однако, в некоторых случаях вегетативные клетки превращаются в гетероцистов. Их распределение следует хорошо наблюдаемому шаблону, в котором соседние гетероцисты разделены примерно одинаковым числом вегетативных клеток. Но как же организм поддерживает постоянное расстояние между гетероцистами во время роста? Предложенная модель описывает этот феномен с точки зрения биологии. Предполагается, что расположение гетероцистов регулируется соединениями азота, производимые этими клетками, которые передаются в другие клетки организма и потребляются в вегетативных клетках. Если содержание этих соединений в молодй вегетативной клетке падает ниже определенного уровня, эта клетка превращается в гетероцист.
L-System ниже моделирует рост бактерии с учетом вышесказанного.
#define присваивает значения константам используемым в L.
#include загружает форму гетероциста, в данном случае круг.
Клетки представлены модулем F(s, t, c), где s — длина клетки, t — тип клетки (0 — гетероцист, 1 и 2 — вегетативные клетки), а c — концентрация азота.
#define CH 900 /* high concentration */
#define CT 0.4 /* concentration threshold */
#define ST 3.9 /* segment size threshold */
#include H /* heterocyst shape specification */
#ignore f ∼ H
ω : -(90)F(0,0,CH)F(4,1,CH)F(0,0,CH)
p1 : F(s,t,c) : t=1 & s>=6 → F(s/3*2,2,c)f(1)F(s/3,1,c)
p2 : F(s,t,c) : t=2 & s>=6 → F(s/3,2,c)f(1)F(s/3*2,1,c)
p3 : F(h,i,k) < F(s,t,c) > F(o,p,r) : s>ST|c>CT → F(s+.1,t,c+0.25*(k+r-3*c))
p4 : F(h,i,k) < F(s,t,c) > F(o,p,r) : !(s>ST|c>CT) → F(0,0,CH) ∼ H(1)
p5 : H(s) : s<3 → H(s*1.1)
Гипножаба.
Вот, например, недавняя гипножаба, покорившая интернет, по сути является комбинацией простейших L.

#define R 1.456
ω : A(1)
p1 : A(s) → F(s)[+A(s/R)][−A(s/R)]Более advanced.
Это всего лишь поверхностное описание теории и небольшие примеры применения на практике. Что ждет любопытного исследователя дальше?
- Моделирование роста двумерных и трехмерных многоклеточных организмов
- Анимация роста организмов деревьев
- Моделирование влияния окружающей среды
- Моделирование химикобиологических процессов и growth functions
- Применение L для генерации поверхностей
- Другие разнообразные варианты использования, в том числе для моделирования недвижимости и городов
Примеры.




Использование.
Еще в конце 80х L использовались для визуализации моделей растений. Сейчас возможности компьютеров ушли далеко вперед. Многие игры и инструменты 3d моделирования используют процедурную генерацию контента, в том числе и L-Systems. Как видите, из набора простых правил можно получить огромное количество разных растений и засадить ими целые поля.
Из редакторов я сам пользуюсь L в Houdini, слышал, что есть плагины и для других пакетов. Так называемая Виртуальная Лаборатория позволяет экспериментировать и анимировать L.
Методы использования грамматик также используются в так называемых Shape Grammars, но об этом потом.
Некоторые посты в интернете.
http://avalter.blogspot.com/2009/08/2d-l.html
Книги и дополнительный материал.
Вообще говоря, единственная доступная книга — это The Algorithmic Beauty of Plants. Также, по интернету разбросаны старые рандомные статьи. Более-менее новые можно найти на springerlink.com за кучу денег или в институтской библиотеке забесплатно.
Что сказать, материала довольно маловато.
Околобиологические мысли.
Я сам имею ровно никакое отношение к биологии, а являюсь Магистром Математики с небольшими невиными увлечениями. Но мне чрезвычайно нравится идея L-Systems. Простота с огромными возможностями. Когда-то давно я задумывался как же так в ДНК содержится полная информация обо мне. Как же можно в каждую клетку впихнуть всю информацию обо всех клетках? А никак, можно сказать, теория L открыла мне глаза! У меня в ДНК написано не как я выгляжу, а как меня собрать (общими словами). Что-то похожее на набор правил в L, только относящееся к синтезу протеинов.
Простая модель так четко описывает нашу с вами жизнь.
Дальше больше — превращаем правила в «ДНК» и генетическим алгоритмом выращиваем виртуальных многоклеточных.
Научные мысли.
Мне бы хотелось найти людей, которые тоже заинтересованы в научной составляющей L, поделиться материалами и статьями. Так уж получилось, что я сейчас работаю над апгрейженной концепцией L-Systems, но не имею возможности просмотреть что писалось по этой теме за последние пять лет. Не хочется изобретать велосипед.
Связаться с автором КНИГИ не удалось, автоответчик говорит, что он уехал на шабаш до января (8
Также, я ищу информацию по Shape Grammars для 3d моделирования. Есть задача генерировать из параметров космические корабли, ну знаете такие огромные штуковины с кучей мелких деталей — идеальные кандидаты для SG. Неужели придется писать плагин для Houdini на Python?






