Статистика — это такой инструмент… Очень страшный в неумелых руках. В умелых того страшнее, способен разорвать мозг на куски.
Вот есть последовательности A, B, C и D, про которые известно следующее:
То есть все указанные величины для них совпадают. По крайней мере, до второго знака после запятой.А теперь смотрим глазами:
Такая вот картина маслом. Можно скачать .XLS с данными для самостоятельного изучения.
Придумал эту штуку британский статистик Ф.Дж. Анскомбе, и называется она «квартет Анскомбе». Поговорку про среднюю температуру по больнице все слышали, а теперь у вас есть к ней хорошая иллюстрация.
Про квартет Анскомбе в английской википедии.
UPD: началось портирование этой статьи в русскую википидею, и там правильно замечают, что автора следует называть Френсис Энскомб.
Вот есть последовательности A, B, C и D, про которые известно следующее:
| A | B | C | D | |
|---|---|---|---|---|
| Среднее значение x | 9.00 | 9.00 | 9.00 | 9.00 |
| Дисперсия х | 10.00 | 10.00 | 10.00 | 10.00 |
| Среднее значение y | 7.50 | 7.50 | 7.50 | 7.50 |
| Дисперсия y | 3.75 | 3.75 | 3.75 | 3.75 |
| Корреляция между x и y | 0.82 | 0.82 | 0.82 | 0.82 |
| Прямая линейной регрессии | y = 3 + 0.5 x | y = 3 + 0.5 x | y = 3 + 0.5 x | y = 3 + 0.5 x |
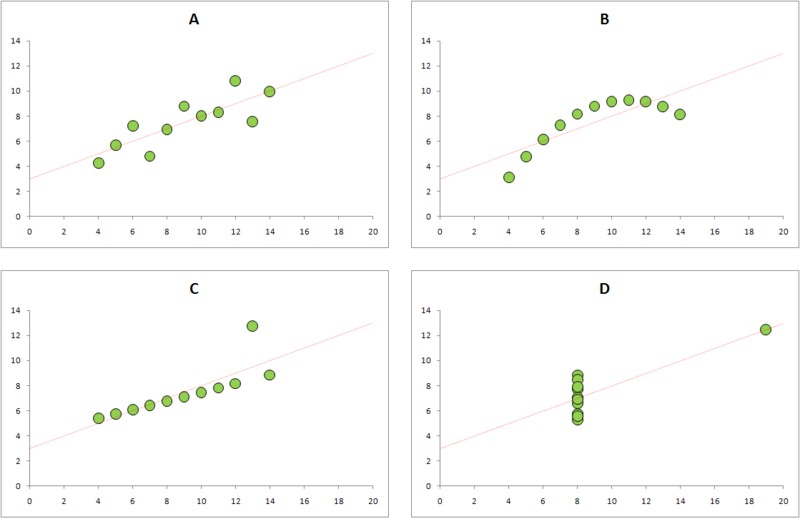
Такая вот картина маслом. Можно скачать .XLS с данными для самостоятельного изучения.
Придумал эту штуку британский статистик Ф.Дж. Анскомбе, и называется она «квартет Анскомбе». Поговорку про среднюю температуру по больнице все слышали, а теперь у вас есть к ней хорошая иллюстрация.
Про квартет Анскомбе в английской википедии.
UPD: началось портирование этой статьи в русскую википидею, и там правильно замечают, что автора следует называть Френсис Энскомб.








